|
|
|
|
|
|
|
  |
 Jul 26 2007, 01:12 AM Jul 26 2007, 01:12 AM
Publicado:
#1
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Aquí tenemos la IMO de este año. Están invitados a postear sus soluciones
48ª OLIMPIADA INTERNACIONAL DE MATEMÁTICA Hanoi, Vietnam, 2007 Primera Prueba: Miércoles 25 de julio de 2007 Problema 1: Sean 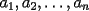 números reales. Para cada números reales. Para cada 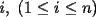 , se define , se define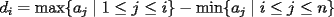 y sea 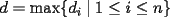 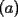 Demuestre que, para cualesquiera Demuestre que, para cualesquiera 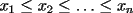 números reales, números reales,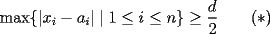 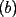 Pruebe que existen números reales Pruebe que existen números reales 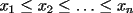 que cumplen la igualdad en que cumplen la igualdad en 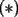 Problema 2: Sean 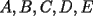 cinco puntos tales que cinco puntos tales que 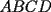 es un paralelógramo y es un paralelógramo y 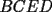 es un cuadrilátero cíclico. Sea es un cuadrilátero cíclico. Sea 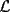 una recta que pasa por una recta que pasa por 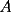 y que corta a y que corta a 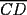 en en 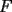 y a y a 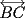 en en 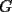 , de modo que , de modo que 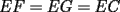 . Pruebe que . Pruebe que 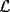 es la bisectriz del es la bisectriz del 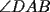 . .Problema 3: En una competencia de matemáticas algunos participantes son amigos. La amistad es siempre mutua. Llamamos a un grupo de participantes pandilla si cualesquiera dos de ellos son amigos. (En particular, cualquier grupo con menos de dos participantes es una pandilla.) El número de miembros de una pandilla es su tamaño. Si en esta competencia, el mayor tamaño de una pandilla es par, demuestre que los participantes pueden colocarse en dos habitaciones de modo que el mayor tamaño de una pandilla contenido en una habitación es el mismo que el mayor tamaño de una pandilla contenido en la otra habitación. Segunda Prueba: Jueves 26 de julio de 2007 Problema 4: En un 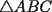 la bisectriz de la bisectriz de 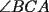 interseca nuevamente al circuncírculo en interseca nuevamente al circuncírculo en 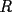 , a la mediatriz de , a la mediatriz de 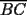 en en 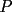 , y a la mediatriz de , y a la mediatriz de 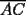 en en 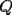 . Sean . Sean 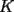 y y 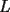 los puntos medios de los puntos medios de 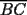 y y 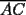 , respectivamente. Pruebe que los triángulos , respectivamente. Pruebe que los triángulos 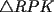 y y 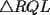 tienen igual área. tienen igual área.Problema 5: Sean 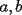 enteros positivos. Demuestre que si enteros positivos. Demuestre que si 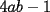 divide a divide a 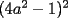 , entonces , entonces 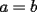 . .Problema 6: Sea  un entero positivo. Considere un entero positivo. Considere 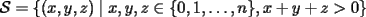 un conjunto de 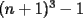 puntos en el espacio tridimensional. Determine el menor número posible de planos cuya unión contiene a puntos en el espacio tridimensional. Determine el menor número posible de planos cuya unión contiene a 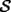 pero no incluye a pero no incluye a 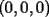 . .Resumen de soluciones -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
 Jul 27 2007, 01:10 AM Jul 27 2007, 01:10 AM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Colaborador Gold Mensajes: 1.118 Registrado: 11-September 05 Desde: Valdivia/Ancud Miembro Nº: 302 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Sean
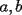 enteros positivos. Demuestre que si enteros positivos. Demuestre que si 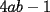 divide a divide a 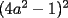 , entonces , entonces 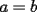 . .Sea 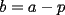 , luego al hacer la división de , luego al hacer la división de 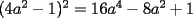 entre entre 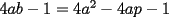 se obtiene cuociente se obtiene cuociente 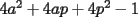 y resto y resto 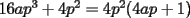 que debe ser nulo. que debe ser nulo.Por lo tanto,  PD: Sí, me pareció interesante una posible solución existente en la red ... Fue un buen intento. A ver quién puede seguir por este mismo camino. Mensaje modificado por JoNy_SaTiE el Jul 28 2007, 01:48 PM -------------------- Comienza a crear documentos con LaTeX.
Ya usas LaTeX y quieres aprender un poco más ... pincha aquí Si eres de la UaCH ... únete a la causa !!! J. Jonathan H. Oberreuter A. Universidad Austral de Chile - RWTH Aachen alumni Est. Magister en Acústica y Vibraciones Ingeniero Civil Acústico (E) Bachiller y Licenciado en Cs. de la Ingeniería |
|
|
|
 Jul 27 2007, 01:26 AM Jul 27 2007, 01:26 AM
Publicado:
#3
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Sean 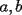 enteros positivos. Demuestre que si enteros positivos. Demuestre que si 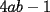 divide a divide a 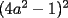 , entonces , entonces 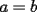 . .Sea 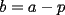 , luego al hacer la división de , luego al hacer la división de 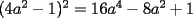 entre entre 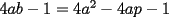 se obtiene cuociente se obtiene cuociente 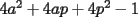 y resto y resto 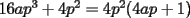 que debe ser nulo. que debe ser nulo.Por lo tanto,  Bonita solución, creo haberla visto en algún foro llamado mathlinks -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
 Jul 27 2007, 09:31 AM Jul 27 2007, 09:31 AM
Publicado:
#4
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 193 Registrado: 22-March 07 Desde: San Miguel, Santiago Miembro Nº: 4.651 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Bonita solución, creo haberla visto en algún foro llamado mathlinks el resto al que llego no debe ser 0, solo llego a un resto que obviamente es divisible por 4ab-1, el problema sigue en pie -------------------- |
|
|
|
 Jul 27 2007, 08:12 PM Jul 27 2007, 08:12 PM
Publicado:
#5
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
el resto al que llego no debe ser 0, solo llego a un resto que obviamente es divisible por 4ab-1, el problema sigue en pie Toda la razón Saludos. -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
 Jul 28 2007, 11:20 AM Jul 28 2007, 11:20 AM
Publicado:
#6
|
|
|
Matemático Grupo: Usuario FMAT Mensajes: 39 Registrado: 8-March 07 Desde: Santiago Miembro Nº: 4.388 Nacionalidad:  Sexo:  |
algo off-topic pero son noticias frescas
CAN3 Yan Li 5 P 0 7 1 0 CAN4 Alexander Remorov 7 P 0 7 1 0 CAN5 Jonathan Timur Schneider 3 P 0 6 0 0 CAN6 Chengyue (Jarno) Sun 3 P 0 7 0 0 CHI1 Cristobal Parraguez 0 1 P 0 1 0 CHI2 Francisco Campos 0 0 P 0 0 0 CHI3 Roberto Villaflor 0 1 P 0 1 0 CHI4 Sebastian Pacheco 0 0 P 0 0 0 CHN1 Han Hu P P P P P 0 CHN2 Xuan Wang P P P P P 1 CHN3 Caili Shen P P P P P 1 CHN4 Tengyu Ma P P P P P 0 CHN5 Ben Yang P P P P P 1 CHN6 Lei Fu P P P P P 0 COL1 Diego Cifuentes 3 1 P P P 0 COL2 Santiago Cuellar 6 2 P P P 0 COL3 Jose Alejandro Samper 7 1 P P P 0 COL4 Miguel Acosta 3 1 P P P 0 la P quiere decir pendiente..... no anduvieron bien las cosas , bien espero que esto calme un poco los pataleos si dejamos de participar en la IMO, yo hare lo posible por que asi sea. -------------------- MP11
www.math.u-psud.fr/~ponce |
|
|
|
 Jul 28 2007, 03:23 PM Jul 28 2007, 03:23 PM
Publicado:
#7
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
algo off-topic pero son noticias frescas CAN3 Yan Li 5 P 0 7 1 0 CAN4 Alexander Remorov 7 P 0 7 1 0 CAN5 Jonathan Timur Schneider 3 P 0 6 0 0 CAN6 Chengyue (Jarno) Sun 3 P 0 7 0 0 CHI1 Cristobal Parraguez 0 1 P 0 1 0 CHI2 Francisco Campos 0 0 P 0 0 0 CHI3 Roberto Villaflor 0 1 P 0 1 0 CHI4 Sebastian Pacheco 0 0 P 0 0 0 CHN1 Han Hu P P P P P 0 CHN2 Xuan Wang P P P P P 1 CHN3 Caili Shen P P P P P 1 CHN4 Tengyu Ma P P P P P 0 CHN5 Ben Yang P P P P P 1 CHN6 Lei Fu P P P P P 0 COL1 Diego Cifuentes 3 1 P P P 0 COL2 Santiago Cuellar 6 2 P P P 0 COL3 Jose Alejandro Samper 7 1 P P P 0 COL4 Miguel Acosta 3 1 P P P 0 la P quiere decir pendiente..... no anduvieron bien las cosas , bien espero que esto calme un poco los pataleos si dejamos de participar en la IMO, yo hare lo posible por que asi sea. ¿Como se supone que vamos a lograr algo importante a Nivel Internacional si no lo intentamos?. Me parece ilogico que dejemos ir por la borda algo que ha costado tanto tiempo recuperar. Hoy en dia era razonable que no teniamos equipo como para ir a una IMO, sin embargo puede ser que con el estimulo de poder ir, eso pueda ir mejorando. En Concepcion se estan preparando cursos para alumnos de alto rendimiento, ahora logramos alargarlo a 3 semanas (antes era de 2), ademas que se estan haciendo esfuerzos para traer algun extranjero para que dicte clases de Olimpiadas. En el pasado no se contaba con un sitio donde se pudiera compartir conocimientos como lo es Fmat (de hecho ni acceso a internet teniamos). Recuerdo que en mis tiempos no tenia ningun libro para aprender mas y tampoco tenia muchos materiales (debia perseguir a mis profesores para que me dieran problemitas). Yo aun tengo fe en que algo puede lograrse en un mediano a largo plazo, pero para que se tomen iniciativas para entrenar a un mas alto nivel, primero tienen que existir las instancias para ir a competir en ese nivel (se pierde un poco el estimulo por aprender mas cosas si no hay ninguna olimpiada en la cual poder usarlo, lo cual no descarta que se pueda hacer solo por placer[de hecho esa es la idea], pero indiscutiblemente en jovenes eso los hace focalizarse mas en temas que tengan que ver con sus competencias). Saludos PD: Estoy de acuerdo que la diferencia es demasiado grande, sin embargo me parece logico que si intentamos en primera instancia aspirar a una IMO, no lo logremos, pero si podamos hacer un mejor papel en la Iberoamericana (y asi ir mejorando). -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Jul 28 2007, 06:33 PM Jul 28 2007, 06:33 PM
Publicado:
#8
|
|
|
Matemático Grupo: Usuario FMAT Mensajes: 39 Registrado: 8-March 07 Desde: Santiago Miembro Nº: 4.388 Nacionalidad:  Sexo:  |
Estimado David, sabes bien que mi opinion sobre la formacion y el trabajo que la gente nueva esta haciendo es muy buena (especialmente tu trabajo en este sitio). Sin embargo creo que este trabajo debe focalizarse en la Ibero, que es donde podemos competir de buena manera, que es una verdadera competencia de talentos y no una profesionalizacion de la resolucion de problemas rebuscados como la IMO. Por ejemplo, el equipo frances este agno tuvo una preparacion impresionante , se juntaron un mes durante todos los dias (de 8 a 22hrs) aqui en Orsay a trabajar, yo les veia y me daba envidia, pero sus resultados igual fueron malos. En cambio, los profesionales de esto siguen sacando buenos puntajes lo que en general no se ve reflejado en mejores resultados a la larga (a nivel de su investigacion en matematica). Este agno ir a la IMO fue casi una obligacion impuesta por el "desatino" de uno de los participantes de este foro al poner en aprietos a la presidenta en publico, y creo que haber sacado casi cero perfecto nos perjudica en lugar de beneficiar a la hora de ir a negociar nuevos recursos. Bien , de todas maneras lo que debe estar claro es que en Chile hay muchisimo potencial y que lo debemos aprovechar y fortalecer, y en eso tu trabajo esta siendo notable.
Un abrazo -------------------- MP11
www.math.u-psud.fr/~ponce |
|
|
|
 Jul 28 2007, 06:45 PM Jul 28 2007, 06:45 PM
Publicado:
#9
|
|
 Máquina que convierte café en teoremas Grupo: Colaborador Silver Mensajes: 1.665 Registrado: 18-August 05 Desde: Concepción Miembro Nº: 247 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Estimado David, sabes bien que mi opinion sobre la formacion y el trabajo que la gente nueva esta haciendo es muy buena (especialmente tu trabajo en este sitio). Sin embargo creo que este trabajo debe focalizarse en la Ibero, que es donde podemos competir de buena manera, que es una verdadera competencia de talentos y no una profesionalizacion de la resolucion de problemas rebuscados como la IMO. Por ejemplo, el equipo frances este agno tuvo una preparacion impresionante , se juntaron un mes durante todos los dias (de 8 a 22hrs) aqui en Orsay a trabajar, yo les veia y me daba envidia, pero sus resultados igual fueron malos. En cambio, los profesionales de esto siguen sacando buenos puntajes lo que en general no se ve reflejado en mejores resultados a la larga (a nivel de su investigacion en matematica). Este agno ir a la IMO fue casi una obligacion impuesta por el "desatino" de uno de los participantes de este foro al poner en aprietos a la presidenta en publico, y creo que haber sacado casi cero perfecto nos perjudica en lugar de beneficiar a la hora de ir a negociar nuevos recursos. Bien , de todas maneras lo que debe estar claro es que en Chile hay muchisimo potencial y que lo debemos aprovechar y fortalecer, y en eso tu trabajo esta siendo notable. Un abrazo Disculpa, pero los que la rompen en la IMO como lo hacen? yo creo que ellos entrenan mucho mas que un mes. La humilde opinion de un estudiante. Saludos --------------------  Manual para subir imágenes y archivos a fmat (con servidor propio) Manual de latex Estilo Propio Lista de libros en fmat    "Un Matemático es una máquina que trasforma café en teoremas"(Erdös) --- Consultas, sugerencias, reclamos via mp o a los correos mencionados. |
|
|
|
 Jul 28 2007, 06:45 PM Jul 28 2007, 06:45 PM
Publicado:
#10
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 765 Registrado: 6-December 05 Miembro Nº: 458 Nacionalidad:  Sexo:  |
Problema 1: Sean 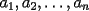 números reales. Para cada números reales. Para cada 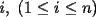 , se define , se define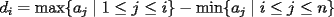 y sea 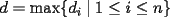 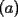 Demuestre que, para cualesquiera Demuestre que, para cualesquiera 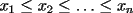 números reales, números reales,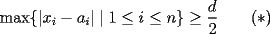 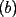 Pruebe que existen números reales Pruebe que existen números reales 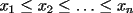 que cumplen la igualdad en que cumplen la igualdad en 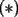 
-------------------- Pasten, un buen muchacho en quien confiar.
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 16th June 2025 - 08:28 AM |










