|
|
|
|
|
|
|
  |
 Jul 28 2007, 06:56 PM Jul 28 2007, 06:56 PM
Publicado:
#11
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 765 Registrado: 6-December 05 Miembro Nº: 458 Nacionalidad:  Sexo:  |
Este agno ir a la IMO fue casi una obligacion impuesta por el "desatino" de uno de los participantes de este foro al poner en aprietos a la presidenta en publico, y creo que haber sacado casi cero perfecto nos perjudica en lugar de beneficiar a la hora de ir a negociar nuevos recursos. Señor MP11, no se hasta que punto fue desatino lo que hice porque contaba con el apoyo de una representante de la SOMACHI, y fue ella misma quien me dio datos concretos para poder discutir. El año pasado habia un equipo bueno y probablemente habriamos vuelto al menos con una mencion, lamentablemente el reglamento de la IMO nos impidio ir por estar los 4 matriculados en una universidad. Si nos estamos automarginando de competencias de alto nivel dificilmente podremos algun dia tener un nivel competitivo. No manejo datos sobre el ambiente futbolistico pero se que este año con un bronce se quedaron todos felices, me imagino que debe ser primera vez en mucho tiempo que Chile regresa con algo, sin embargo nadie le niega la oportunidad de competir a los futbolitas chilenos.. claro, al tratarse del "furbo" no falta plata. Sobre ese comentario de "espero que esto calme un poco los pataleos si dejamos de participar en la IMO, yo hare lo posible por que asi sea"... no sera que mucho tiempo fuera de Chilito nos esta cambiando el equipo? Si no nos apoyamos entre chilenos, ufff... se ve negro el futuro. Saludos -------------------- Pasten, un buen muchacho en quien confiar.
|
|
|
|
 Jul 28 2007, 07:10 PM Jul 28 2007, 07:10 PM
Publicado:
#12
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 691 Registrado: 2-December 06 Miembro Nº: 3.105 |
no se nada de olimpiadas, pero opino que podrian pedirle a los rusos que se pasasen el dato jesus christ
http://www.imo2007.edu.vn/index.php?module=ViewRank |
|
|
|
 Jul 28 2007, 07:19 PM Jul 28 2007, 07:19 PM
Publicado:
#13
|
|
|
Matemático Grupo: Usuario FMAT Mensajes: 39 Registrado: 8-March 07 Desde: Santiago Miembro Nº: 4.388 Nacionalidad:  Sexo:  |
En los argumentos del tipo "automarginarnos de competencias de alto nivel no nos permitira tener un buen nivel" caemos en el error (u omision) de suponer que los objetivos de las competencias estan claros. Una parte de la SOMACHI tiene algunos objetivos, otra parte tiene otros un poco diferentes y algunos de los que ya estamos hace tiempo "cambiandonos de equipo" quizas solo sea que tenemos otros aun mas diferentes para las competencias. Al menos quienes hemos creado un grupo de investigadores jovenes con pasado olimpico queremos que los jovenes talentosos como tu tengan al menos las mismas oportunidades que se nos dieron a nosotros de hacer investigacion de primer nivel, y por lo menos yo creo que gastando nuestros esfuerzos en ir a la IMO no vamos por buen camino, las energias son escasas y deberian apuntar en abrir puertas y no en colgarse medallas a punta de conocer teoremas rebuscados. Por lo menos yo no respeto la IMO, debe ser porque conozco a muchos que se han colgado medallas y que hoy las cambiarian sin dudar por haber estado en Chile bajo la guia de quienes nos proporcionaron las oportunidades para hacer matematica de verdad.
-------------------- MP11
www.math.u-psud.fr/~ponce |
|
|
|
 Jul 28 2007, 07:27 PM Jul 28 2007, 07:27 PM
Publicado:
#14
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 765 Registrado: 6-December 05 Miembro Nº: 458 Nacionalidad:  Sexo:  |
En los argumentos del tipo "automarginarnos de competencias de alto nivel no nos permitira tener un buen nivel" caemos en el error (u omision) de suponer que los objetivos de las competencias estan claros. Una parte de la SOMACHI tiene algunos objetivos, otra parte tiene otros un poco diferentes y algunos de los que ya estamos hace tiempo "cambiandonos de equipo" quizas solo sea que tenemos otros aun mas diferentes para las competencias. Al menos quienes hemos creado un grupo de investigadores jovenes con pasado olimpico queremos que los jovenes talentosos como tu tengan al menos las mismas oportunidades que se nos dieron a nosotros de hacer investigacion de primer nivel, y por lo menos yo creo que gastando nuestros esfuerzos en ir a la IMO no vamos por buen camino, las energias son escasas y deberian apuntar en abrir puertas y no en colgarse medallas a punta de conocer teoremas rebuscados. Por lo menos yo no respeto la IMO, debe ser porque conozco a muchos que se han colgado medallas y que hoy las cambiarian sin dudar por haber estado en Chile bajo la guia de quienes nos proporcionaron las oportunidades para hacer matematica de verdad. Perdon por lo cargante, pero tu si pudiste ir a una imo y ahora estas haciendo investigacion, y no eres el unico. No veo la incompatibilidad entre apoyar la participacion en competencias y hacer investigacion matematica. Es mas, si antes se pudo no veo el problema con dar la misma oportunidad a los jovenes de ahora, con la mala suerte que partimos con una generacion mala y una prueba mas complicada que otros años, pero a futuro quisas no sea el caso. -------------------- Pasten, un buen muchacho en quien confiar.
|
|
|
|
 Jul 28 2007, 07:42 PM Jul 28 2007, 07:42 PM
Publicado:
#15
|
|
|
Matemático Grupo: Usuario FMAT Mensajes: 39 Registrado: 8-March 07 Desde: Santiago Miembro Nº: 4.388 Nacionalidad:  Sexo:  |
No te preocupes, aun no tengo tantos medios como para que me pesquen para tomar ese tipo de decisiones, sin embargo debes tener claro que si quieres que Chile vaya a la IMO debes estar dispuesto a trabajar duro para preparar equipos, ya hablaremos personalmente uno de estos dias.
Para terminar , cuando Chile fue a la IMO en los 90's , eramos protagonistas en la Ibero, la generacion de Rivera, Navas y M. Libedinski y las que habian estado antes se ganaron el derecho a intentarlo, nosotros nos aprovechamos de eso (y no nos fue muy bien). No me estoy lavando las manos de nada, de hecho muchas veces pienso que el momento en que las generaciones chilenas empezaron a ser mas debiles coincide fortuitamente con el momento en que las empece a entrenar yo, veamos que pasara ahora..... -------------------- MP11
www.math.u-psud.fr/~ponce |
|
|
|
 Jul 28 2007, 08:16 PM Jul 28 2007, 08:16 PM
Publicado:
#16
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 765 Registrado: 6-December 05 Miembro Nº: 458 Nacionalidad:  Sexo:  |
Problema 4: En un 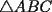 la bisectriz de la bisectriz de 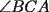 interseca nuevamente al circuncírculo en interseca nuevamente al circuncírculo en 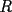 , la mediatriz de , la mediatriz de 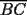 lo hace en lo hace en 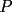 y la mediatriz de y la mediatriz de 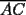 en en 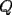 . Sean . Sean 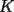 y y 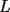 los puntos medios de los puntos medios de 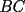 y y 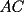 , respectivamente. Pruebe que las áreas de los triángulos , respectivamente. Pruebe que las áreas de los triángulos 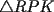 y y 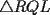 son iguales. son iguales.Mal traducido... P es la interseccion de CR con la mediatriz de BC, analogo para Q.  
-------------------- Pasten, un buen muchacho en quien confiar.
|
|
|
|
| Cesarator |
 Jul 28 2007, 09:55 PM Jul 28 2007, 09:55 PM
Publicado:
#17
|
|
Invitado |
Primero, felicitar al equipo chileno por su esfuerzo, no quiero que se piense que aquí los estamos "haciendo polvo".
Fueron a competir con la elite mundial, los lleva la SOMACHI, que no los prepara de ninguna manera y los selecciona a última hora. Esto es una fuerte (auto) crítica. Y, desde ya, si una actividad lleva a la reflexión, es positiva. Tuvieron la oportunidad de conocer gente, y de sentirse muuuy pequeños, un baño de humildad muy bueno para su desarrollo personal. Segundo, felicitar mucho al espectacular rendimiento del equipo peruano. Si alguno de los integrantes de ese equipo pasa por aquí: ESPECTACULAR, maestros. Estan entre los grandes. Favor, si alguno de los integrantes del sistema peruano pasa por aquí, contactarme por MP, pues quiero saber como hacen ustedes las cosas y, humildemente, aprender de ustedes. Tercero. Otra gran y muy gran felicitación al equipo colombiano y, lo mismo. Latinoamérica se ve presente y, en este momento, ustedes son los TOP. Esto también espero inspire a nuestro país y nos otorgue la humildad suficiente para pedirles consejo a los responsables de estas naciones, no tan lejanas, no tan diferentes a Chile. Con respecto a si conviene participar o no participar, parece una discusión un poco estéril. De partida, es un poco ambiguo el concepto de, por ejemplo, "prepararse para la ibero". En general, entiendo que un equipo se prepara, y la preparación servirá para cualquier competencia. Tampoco veo cómo ir a la mundial hace "gastar recursos que podrían ocuparse en otra cosa". Eso es un tema enteramente de gestión administrativa y, créanme, el problema actual de nuestro país No es del recurso PLATA. Siendo movido, la plata se consigue (como quedó demostrado con la ida a la mundial de este año). Además, estoy seguro que si la plata de los pasajes de la mundial no se gastaba justamente en ir a la mundial, simplemente se perdía: es muy distinto pedir recursos para ir a una mundial que para ir a una ibero. Es como pedir una beca para estudiar un magister y no un doctorado. La beca de magister es más chica y más dificil de ganar, la del doctorado es más grande y, creanme, es más fácil obtener una beca para un doctorado que para un magister. Completo, el problema no es la plata, es la gente. Nuestra comunidad matemática no hace entrenamientos sistemáticos. Esa comunidad de "Jovenes matemáticos ex olímpicos", perdón, pero ¿Donde entrenan? ¿Cuántas veces a la semana lo hace? No se me tome a mal, yo estoy en este momento "buscando entrenadores" chilenos y, sinceramente, no conozco más que 2 o 3 (dar unas cuantas "charlas motivacionales" las hace cualquiera con conocimento para ello, pero diseñar un cursillo de 3 semanas de preparación olímpica ¿quién lo hace en Chile? ). Y el problema de "formar nuevos matemáticos"... uy, problema complejo de nivel país. Cada vez hay menos Licenciaturas en matemática en Chile pero, favor tener mucho cuidado, hay lugares que estomos creciendo con respecto a ello, y las olimpiadas ayudan mucho. En fin, tema para largo pero, en general, hay que estar conciente que siempre acciones del tipo "voy a hacer todas las gestiones para que esta actividad no se realice más" aparecen como negativas. Si se aspira a tener medalla de oro en la IMo, claro, nunca será, pero estar entre los 50 primeros, con la posibilidad que los cabros talentosos (como los que fueron) si puedan aspirar a un broncecito y desarrollar su potencialidad, no tiene nada de malo ni parece un despilfarro de recursos de ningún tipo. La IMo se ha utilizado mal administrativamente, y me parece que es mucho más fácil conseguir recursos, trabajar motivando gente con IMO que sin IMO, pero well, puedo estar equivocado. |
|
|
|
 Aug 3 2007, 11:03 PM Aug 3 2007, 11:03 PM
Publicado:
#18
|
|
 Máquina que convierte café en teoremas Grupo: Colaborador Silver Mensajes: 1.665 Registrado: 18-August 05 Desde: Concepción Miembro Nº: 247 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Desempeño latino en la IMO 2007.
1) Brazil (106 puntos) (2 platas, 3 bronces) 2) Colombia (93 puntos) (1 plata, 3 bronces) 3) Peru (91 puntos) (1 plata, 2 bronces) 4) Mexico (86 puntos) (4 bronces) 5) Argentina (75 puntos) (1 plata, 1 bronce) 6) Chile... Definitivamente se debe mejorar --------------------  Manual para subir imágenes y archivos a fmat (con servidor propio) Manual de latex Estilo Propio Lista de libros en fmat    "Un Matemático es una máquina que trasforma café en teoremas"(Erdös) --- Consultas, sugerencias, reclamos via mp o a los correos mencionados. |
|
|
|
 Aug 4 2007, 08:35 PM Aug 4 2007, 08:35 PM
Publicado:
#19
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
No me había animado a postear la solución a este problema, ya que es muy larga y he andado corto de tiempo. Agradezco a uno de los IMOers chilenos por su hint que me llevó a la solución
Problema 2: Sean 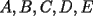 cinco puntos tales que cinco puntos tales que 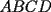 es un paralelógramo y es un paralelógramo y 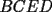 es un cuadrilátero cíclico. Sea es un cuadrilátero cíclico. Sea 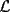 una recta que pasa por una recta que pasa por 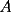 y que corta a y que corta a 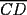 en en 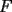 y a y a 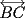 en en 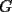 , de modo que , de modo que 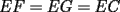 . Pruebe que . Pruebe que 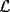 es la bisectriz del es la bisectriz del 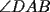 . .Solución al problema 2 Lema: Considere los datos del enunciado. Sea 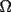 la circunferencia circunscrita al cuadrilátero cíclico la circunferencia circunscrita al cuadrilátero cíclico 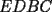 . Entonces . Entonces 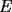 es el punto medio del arco es el punto medio del arco 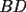 que contiene a que contiene a 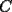 en en 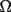 Demostración del lema  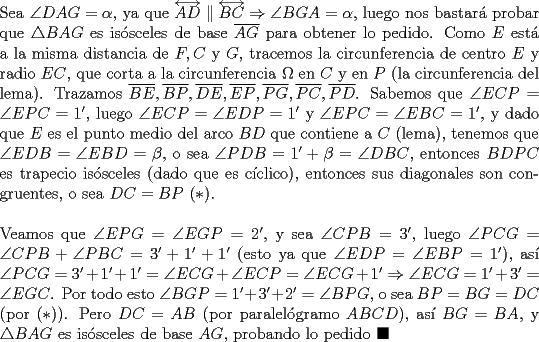 Saludos PD: en la figura omití muchos datos porque me quedaba muy cargada y se confundían las cosas. -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
 Aug 7 2007, 04:45 PM Aug 7 2007, 04:45 PM
Publicado:
#20
|
|
 Matemático Grupo: Usuario FMAT Mensajes: 40 Registrado: 19-July 06 Desde: Conce, Jazz Capitol Miembro Nº: 1.716 Nacionalidad:  Sexo:  |
Una solución para los que somos negados en transformaciones
  Puede demostrarse el siguiente recíproco del problema:  Esto tiene una solución mas simple y creo que sería interesante ver si alguien puede usar este hecho para resolver el problema de otra forma (estuve un buen rato tratando de buscar cómo pero no pude llegar a nada concreto Salu2 |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 16th June 2025 - 04:28 PM |













