|
|
|
|
|
|
|
  |
 Jan 5 2008, 04:06 PM Jan 5 2008, 04:06 PM
Publicado:
#21
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.920 Registrado: 19-August 06 Desde: DIM, DCC Beauchef Miembro Nº: 1.989 Nacionalidad:  Universidad:  Sexo:  |
Problema 6: Sea  un entero positivo. Considere un entero positivo. Considere 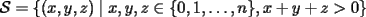 un conjunto de 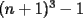 puntos en el espacio tridimensional. Determine el menor número posible de planos cuya unión contiene a puntos en el espacio tridimensional. Determine el menor número posible de planos cuya unión contiene a 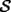 pero no incluye a pero no incluye a 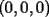 . .Mil disculpas si quiero revivir este tema. Creo que hay un teorema en Álgebra que soluciona en pocas líneas este problema. El problema en ese caso es demostrar el teorema. -------------------- Miembro de Anime No Seishin Doukokai, podrías ser el próximo.
|
|
|
|
 Jan 14 2008, 07:01 PM Jan 14 2008, 07:01 PM
Publicado:
#22
|
|
 Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 21 Registrado: 22-October 06 Desde: SJL - Lima Miembro Nº: 2.613 Nacionalidad:  Sexo:  |
Primero, felicitar al equipo chileno por su esfuerzo, no quiero que se piense que aquí los estamos "haciendo polvo". Fueron a competir con la elite mundial, los lleva la SOMACHI, que no los prepara de ninguna manera y los selecciona a última hora. Esto es una fuerte (auto) crítica. Y, desde ya, si una actividad lleva a la reflexión, es positiva. Tuvieron la oportunidad de conocer gente, y de sentirse muuuy pequeños, un baño de humildad muy bueno para su desarrollo personal. Segundo, felicitar mucho al espectacular rendimiento del equipo peruano. Si alguno de los integrantes de ese equipo pasa por aquí: ESPECTACULAR, maestros. Estan entre los grandes. Favor, si alguno de los integrantes del sistema peruano pasa por aquí, contactarme por MP, pues quiero saber como hacen ustedes las cosas y, humildemente, aprender de ustedes. Tercero. Otra gran y muy gran felicitación al equipo colombiano y, lo mismo. Latinoamérica se ve presente y, en este momento, ustedes son los TOP. Esto también espero inspire a nuestro país y nos otorgue la humildad suficiente para pedirles consejo a los responsables de estas naciones, no tan lejanas, no tan diferentes a Chile. Con respecto a si conviene participar o no participar, parece una discusión un poco estéril. De partida, es un poco ambiguo el concepto de, por ejemplo, "prepararse para la ibero". En general, entiendo que un equipo se prepara, y la preparación servirá para cualquier competencia. Tampoco veo cómo ir a la mundial hace "gastar recursos que podrían ocuparse en otra cosa". Eso es un tema enteramente de gestión administrativa y, créanme, el problema actual de nuestro país No es del recurso PLATA. Siendo movido, la plata se consigue (como quedó demostrado con la ida a la mundial de este año). Además, estoy seguro que si la plata de los pasajes de la mundial no se gastaba justamente en ir a la mundial, simplemente se perdía: es muy distinto pedir recursos para ir a una mundial que para ir a una ibero. Es como pedir una beca para estudiar un magister y no un doctorado. La beca de magister es más chica y más dificil de ganar, la del doctorado es más grande y, creanme, es más fácil obtener una beca para un doctorado que para un magister. Completo, el problema no es la plata, es la gente. Nuestra comunidad matemática no hace entrenamientos sistemáticos. Esa comunidad de "Jovenes matemáticos ex olímpicos", perdón, pero ¿Donde entrenan? ¿Cuántas veces a la semana lo hace? No se me tome a mal, yo estoy en este momento "buscando entrenadores" chilenos y, sinceramente, no conozco más que 2 o 3 (dar unas cuantas "charlas motivacionales" las hace cualquiera con conocimento para ello, pero diseñar un cursillo de 3 semanas de preparación olímpica ¿quién lo hace en Chile? ). Y el problema de "formar nuevos matemáticos"... uy, problema complejo de nivel país. Cada vez hay menos Licenciaturas en matemática en Chile pero, favor tener mucho cuidado, hay lugares que estomos creciendo con respecto a ello, y las olimpiadas ayudan mucho. En fin, tema para largo pero, en general, hay que estar conciente que siempre acciones del tipo "voy a hacer todas las gestiones para que esta actividad no se realice más" aparecen como negativas. Si se aspira a tener medalla de oro en la IMo, claro, nunca será, pero estar entre los 50 primeros, con la posibilidad que los cabros talentosos (como los que fueron) si puedan aspirar a un broncecito y desarrollar su potencialidad, no tiene nada de malo ni parece un despilfarro de recursos de ningún tipo. La IMo se ha utilizado mal administrativamente, y me parece que es mucho más fácil conseguir recursos, trabajar motivando gente con IMO que sin IMO, pero well, puedo estar equivocado. Hola, que tal, mi nombre es Claudio Espinoza, soy un exolimpico peruano desde el 2001,cuando fui a mi primera olimpiada , justamente en Chile, hasta el 2005 que fui a mi ultima participacion en Colombia. Actualmente soy parte de la comision de Olimpiadas de la SMP en Perú y he sido lider en la Cono 2007 y Rio 2007. Si quieres saber sobre la experiencia peruana puedes avisarme, no entiendo que es eso de MP? me avisas. Mensaje modificado por Claudio Espinoza el Jan 14 2008, 07:06 PM |
|
|
|
 Jan 15 2008, 01:57 PM Jan 15 2008, 01:57 PM
Publicado:
#23
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Hola, que tal, mi nombre es Claudio Espinoza, soy un exolimpico peruano desde el 2001,cuando fui a mi primera olimpiada , justamente en Chile, hasta el 2005 que fui a mi ultima participacion en Colombia. Actualmente soy parte de la comision de Olimpiadas de la SMP en Perú y he sido lider en la Cono 2007 y Rio 2007. Si quieres saber sobre la experiencia peruana puedes avisarme, no entiendo que es eso de MP? me avisas. Lamentablemente, Cesarator ha dejado de participar en este foro. Todos le deseamos mucho éxito en sus actividades, para que siga aportando al desarrollo de la matemática en Chile (y América Latina). Él ha partido de fmat, pero aquí seguimos existiendo personas interesadas en la experiencia peruana. Me gustaría conocer detalles, y por eso te pido que los compartas con nosotros (también soy ex olímpico, participé de la Cono Sur 1998, la Cono Sur 2000 y la Iberoamericana 2001, y estoy conciente del buen nivel de las delegaciones peruanas, y su evolución en los últimos años). Si decides compartir esta experiencia, puedes elegir entre responder en este tema o, si prefieres, enviarme un mensaje personal (MP es una abreviación de Mensaje Personal). En caso que Cesarator siga interesado, intentaré mantenerlo informado. Un saludo -------------------- |
|
|
|
 Jan 25 2008, 04:19 PM Jan 25 2008, 04:19 PM
Publicado:
#24
|
|
|
Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 17 Registrado: 17-January 08 Miembro Nº: 14.766 Sexo:  |
Problema 1: Sean 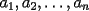 números reales. Para cada números reales. Para cada 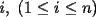 , se define , se define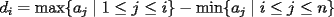 y sea 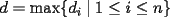 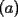 Demuestre que, para cualesquiera Demuestre que, para cualesquiera 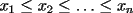 números reales, números reales,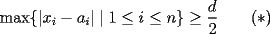 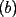 Pruebe que existen números reales Pruebe que existen números reales 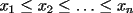 que cumplen la igualdad en que cumplen la igualdad en 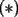 _Si nos fijamos bien, notaremos que ![TEX: \[d\]](./tex/7a8f09d7937935867ee4ad90d194dd54.png) representa la longitud de un segmento de la recta real cuyos extremos son el máximo y el mínimo de representa la longitud de un segmento de la recta real cuyos extremos son el máximo y el mínimo de ![TEX: \[\left\{ {a_i } \right\}_{i = 1}^n \]](./tex/4a8ed75fe5c83eea941a05f21f5c7581.png) . Entonces, es obvio que si ninguno de los . Entonces, es obvio que si ninguno de los ![TEX: \[\left\{ {x_i } \right\}_{i = 1}^n \]](./tex/596882320b9d7e331336689f3eeae321.png) pertenece a dicho segmento, el supremo de las distancias posibles entre un pertenece a dicho segmento, el supremo de las distancias posibles entre un ![TEX: \[x_i\]](./tex/0ed93d112a3806a0b4be89262e758d41.png) y un y un ![TEX: \[a_i\]](./tex/a6d14789627dcb46e4d49fcb52c75cc0.png) será será ![TEX: \[d > d/2\]](./tex/730e37c74279416b911dcc466257fa01.png) , que corresponde (numéricamente) a cuando los , que corresponde (numéricamente) a cuando los ![TEX: \[x_i\]](./tex/b53a689b84066d595fdc5bf87c426622.png) son todos menores que cada son todos menores que cada ![TEX: \[a_i\]](./tex/f35c7f0d07cb51fdcf21c2d8a257e160.png) , ó, cuando todos son mayores que cada , ó, cuando todos son mayores que cada ![TEX: \[a_i\]](./tex/f58fa0cf66db04f92e54900e0f9f0591.png) . ._El caso no trivial ocurre si alguno o todos los ![TEX: \[x_i\]](./tex/f339ae888d5e85ae52ca0951aa51ac55.png) están contenidos en el segmento, de manera que la distancia máxima entre un están contenidos en el segmento, de manera que la distancia máxima entre un ![TEX: \[a_i\]](./tex/be2e248c78d901b60e21a7c90cbdee7c.png) y un y un ![TEX: \[x_i\]](./tex/a3b34c38d761b3cdbd902d47418c836e.png) será siempre mayor que será siempre mayor que ![TEX: \[\tfrac{d}{2}\]](./tex/660e3a5a5eda592bb26b299ebaca648d.png) ; ó, bien, si todos los ; ó, bien, si todos los ![TEX: \[x_i\]](./tex/54a5d65be92810752e77718b81f6be35.png) son iguales y están precisamente en el punto medio del segmento, tendremos que la mayor distancia entre un son iguales y están precisamente en el punto medio del segmento, tendremos que la mayor distancia entre un ![TEX: \[a_i\]](./tex/5e17d2615983005fe71327f152815796.png) y el único y el único ![TEX: \[x_i\]](./tex/e18683822dbb720b37951b286ffe9166.png) será idénticamente igual a será idénticamente igual a ![TEX: \[\tfrac{d}{2}\]](./tex/8f55f02ffd332e80771534dd1208727e.png) . ._Supongo que me doy a entender cuando digo que este problema no requiere de mucha inventiva, así que no me pondré a explicar el proceso de este en particular. _Además, creo que Killua pudo haberlo tipeado más claramente. Cuando se escribe: ![TEX: \[<br />\max \left\{ {\left. {\left| {x_i - a_i } \right|} \right|\;1 \leqslant i \leqslant n} \right\}<br />\]](./tex/385e7bd58b27f5694f921d6e3d7a7327.png) , se da a entender que las diferencias se toman con el mismo orden indicado, o sea, ![TEX: \[x_1\]](./tex/59a6ce3e6c9d2ec1127491db1839f802.png) con con ![TEX: \[a_1\]](./tex/5efd33e1221387d140f73be641009d01.png) , y así sucesivamente. Pudiste haber puesto subíndices distintos a cada letra, para evitar confuciones. Claro está, si los subíndices fuesen los mismos quién diseñó el enunciado se habría equivocado (cosa que no creo posible, pero que sería "posible"), ya que bastaría con redefinir alguna de las dos secuencias para obtener un máximo menor que , y así sucesivamente. Pudiste haber puesto subíndices distintos a cada letra, para evitar confuciones. Claro está, si los subíndices fuesen los mismos quién diseñó el enunciado se habría equivocado (cosa que no creo posible, pero que sería "posible"), ya que bastaría con redefinir alguna de las dos secuencias para obtener un máximo menor que ![TEX: \[\tfrac{d}{2}\]](./tex/3e305d897584090e2045317d1bb12cd3.png) , por tanto, contradiciendo el enunciado a demostrar. , por tanto, contradiciendo el enunciado a demostrar.[E-5] |
|
|
|
 Jan 17 2014, 04:52 PM Jan 17 2014, 04:52 PM
Publicado:
#25
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 81 Registrado: 10-November 12 Miembro Nº: 112.735 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
Pal 4
Saludos :* |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 16th June 2025 - 04:31 PM |






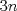 , ¿está correcto?
, ¿está correcto?



