|
|
|
|
|
|
|
  |
| nico |
 May 13 2005, 03:41 AM May 13 2005, 03:41 AM
Publicado:
#1
|
|
Invitado |
Hola, mi nombre es Nicolás Inostroza sali el año pasado de cuarto y soy aficionado a las matemáticas jejeje...este set de preguntas están especialmente dedicadas al grupo de matemáticas de 7º y 8º de los SSCC, pero me gustaria invitar a los q les interesa esto de las olimpiadas que se den el trabajo de leerlos al menos, pues son problemas bastante interesantes...
Esta prueba la tomé en el grupo de olimpíadas hace algun tiempo, me gustaría q trataran de rehacerla, o hacerla en su defecto, todos aquellos que participan del taller... P1)(Clasificación a la Olimpiada Nacional año 2001): En una ruleta circular se colocan los números del 1 al 36 al azar. Demuestre que necesariamente debe haber tres números consecutivos cuya suma sea al menos 55. Hint: trate de ver que es imposible que no haya tres números consecutivos cuya suma sea al menos 55, es decir, trate de probar que lo contrario nunca ocurre(demostración por contradicción). P2)(Clasificación a la Olimpíada Nacional año 2001): Juan nació antes del año 2000. El 25 de agosto del año 2001 cumple tantos años como es la suma de los dígitos del año de su nacimiento. Determine su fecha de nacimiento y justifique que es la única posible. P3)(Clasificación a la Olimpíada Nacional año 2001): Demuestre que no existen números naturales 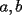 y y  tales que satisfagan lo siguiente: tales que satisfagan lo siguiente: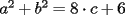 Hint: Vea q pasa con la paridad de los números. ** otros problemas interesantes: P1*)Pruebe que en un grupo de 10 personas, siempre hay al menos dos que tienen el mismo número de amigos dentro del grupo. Vea que esto se cumple para cualquier grupo de personas mayor o igual 2 . P2*)Considere la ordenación de los primeros  números enteros positivos: números enteros positivos: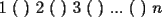 ¿Es posible colocar signos + o signos - dentro de cada ( ), de modo que al efectuar la operación resultante se obtenga 0 como resultado final? P3*)En un tablero cuadrado de lado par, se colocan fichas rectangulares de tamaño 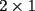 (fichas de dominó). Demuestre que si llenamos el tablero colocando fichas de modo que no me queden una sobre la otra, entonces el número de fichas dispuestas horizontalmente es par. (fichas de dominó). Demuestre que si llenamos el tablero colocando fichas de modo que no me queden una sobre la otra, entonces el número de fichas dispuestas horizontalmente es par.P4*) ¿cuanto vale la suma 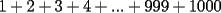 ? ?La solución a cada uno de los problemas será posteada en breve...notar que lo importante no son resultados sino explicar porque suceden las cosas...mucha suerte!!!! |
|
|
|
 May 13 2005, 03:48 AM May 13 2005, 03:48 AM
Publicado:
#2
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Excelentisimo aporte!!!!...asi que ya saben...a postear muchachos...a ver quien sabe resolver estos problemas...saludos
David ^.^ |
|
|
|
 May 14 2005, 02:33 PM May 14 2005, 02:33 PM
Publicado:
#3
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 90 Registrado: 14-May 05 Desde: 33º30'S 70º40'O Miembro Nº: 18 Nacionalidad:  Colegio/Liceo:  Sexo:  |
CITA(nico @ May 13 2005, 04:41 AM) P1*)Pruebe que en un grupo de 10 personas, siempre hay al menos dos que tienen el mismo número de amigos dentro del grupo. Vea que esto se cumple para cualquier grupo de personas mayor o igual 2 Si se agrupan a las personas por la cantidad de amigos, pueden quedar en los siguientes grupos: 0 amigos 1 Amigo 2 Amigos 3 Amigos . . . Hasta el grupo de 9 amigos, porque nadie puede ser amigo de sí mismo Como la amistad es recíproca, es decir, si A es amigo de B, B es amigo de A, no puede haber nadie en el grupo de 9 Amigos y alguien en el de 0 a la vez. Esto nos deja con un grupo menos, hay 10 personas y 9 grupos para agruparlas, entonces tiene que haber al menos un grupo con al menos dos personas. -------------------- "El único primo congruente a uno en módulo cuatro es cinco" A. Gajardo
""I'm going to try to see if I can remember as much to make it sound like I'm smart on the subject."—G. W. Bush, answering a question concerning a possible flu pandemic, Cleveland, July 10, 2007 "I aim to be a competitive nation."—G. W. Bush, San Jose, Calif., April 21, 2006 "Those who enter the country illegally violate the law."— G. W. Bush, Tucson, Ariz., Nov. 28, 2005 "Our enemies are innovative and resourceful, and so are we. They never stop thinking about new ways to harm our country and our people, and neither do we." — G. W. BushWashington, D.C., Aug. 5, 2004 |
|
|
|
 May 14 2005, 02:46 PM May 14 2005, 02:46 PM
Publicado:
#4
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 90 Registrado: 14-May 05 Desde: 33º30'S 70º40'O Miembro Nº: 18 Nacionalidad:  Colegio/Liceo:  Sexo:  |
CITA(nico @ May 13 2005, 04:41 AM) P4*) ¿cuanto vale la suma 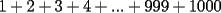 ? ?Una forma de sumar más fácil es asociando de la siguiente forma: 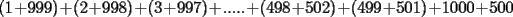 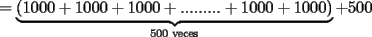 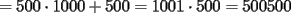 -------------------- "El único primo congruente a uno en módulo cuatro es cinco" A. Gajardo
""I'm going to try to see if I can remember as much to make it sound like I'm smart on the subject."—G. W. Bush, answering a question concerning a possible flu pandemic, Cleveland, July 10, 2007 "I aim to be a competitive nation."—G. W. Bush, San Jose, Calif., April 21, 2006 "Those who enter the country illegally violate the law."— G. W. Bush, Tucson, Ariz., Nov. 28, 2005 "Our enemies are innovative and resourceful, and so are we. They never stop thinking about new ways to harm our country and our people, and neither do we." — G. W. BushWashington, D.C., Aug. 5, 2004 |
|
|
|
 May 14 2005, 02:57 PM May 14 2005, 02:57 PM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Las dos respuestas están bien, en cuanto a la primera, sólo queda ver si esto se cumple para cualquier grupo de personas mayor o igual que 2... por supuesto que la idea es la misma.
Les regalo otro problema para este nivel, dado que estamos sacando problemas de olimpiadas nacionales nivel menor, colaboraré con uno... tienen que saber resolver el problema P4*, espero que sea apreciado este aporte Aquí va el problema (literalmente de la prueba) Se dispone de 1999 bolitas numeradas del 1 al 1999. Encontrar todos los enteros positivos 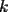 con la siguiente propiedad: el total de bolitas se puede separar en con la siguiente propiedad: el total de bolitas se puede separar en 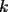 grupos, de modo que la suma de los números de las bolitas en cada uno de los grupos sea la misma. grupos, de modo que la suma de los números de las bolitas en cada uno de los grupos sea la misma.
-------------------- |
|
|
|
| Anonymous |
 May 14 2005, 04:53 PM May 14 2005, 04:53 PM
Publicado:
#6
|
|
Invitado |
CITA(nico @ May 13 2005, 04:41 AM) P3) Demuestre que no existen números naturales 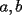 y y  tales que satisfagan lo siguiente: tales que satisfagan lo siguiente: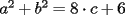 SOL: Sea  y y 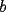 enteros positivos pares, enteros positivos pares, 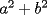 es divisible por 4 ya que es divisible por 4 ya que 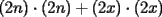 es de la forma es de la forma 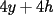 , la suma de dos numeros divisibles por 4 es divisible por 4. Por tanto la ecuacion queda de la siguiente manera: , la suma de dos numeros divisibles por 4 es divisible por 4. Por tanto la ecuacion queda de la siguiente manera: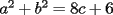 , sabemos que , sabemos que 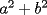 es divisible por 4, es divisible por 4, 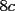 tambien, pero 6 no, por tanto tambien, pero 6 no, por tanto  y y 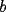 no pueden ser enteros positivos pares. no pueden ser enteros positivos pares.Sea  y y 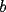 enteros positivos impares, enteros positivos impares, 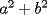 es de la forma es de la forma 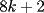 ya que si ya que si  fuera impar, entonces fuera impar, entonces  seria de la forma seria de la forma 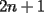 . Ahora notemos que . Ahora notemos que 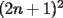 es es 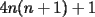 , y , y 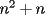 siempre es par (ya que si siempre es par (ya que si  es par , es par , 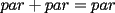 ; y si fuera impar , ; y si fuera impar , 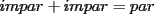 ), a lo que llamaremos ), a lo que llamaremos 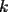 (constante par). (constante par).Por lo tanto 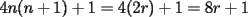 Analogamente 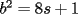 Asi 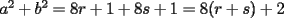 Llamando 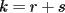 obtendremos: obtendremos: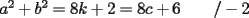 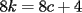 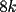 es divisible por 8, es divisible por 8, 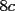 es divisible por 8, pero 4 no es divisible por 8, por tanto la ecuacion no tienen soluciones enteras positivas. es divisible por 8, pero 4 no es divisible por 8, por tanto la ecuacion no tienen soluciones enteras positivas.Sea  par y par y 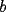 impar, impar, 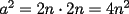 , que es un numero par, a su vez , que es un numero par, a su vez  que seria un numero impar, por otro lado que seria un numero impar, por otro lado 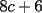 es un numero par; por tanto la ecuacion queda de la siguiente manera: es un numero par; por tanto la ecuacion queda de la siguiente manera: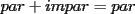 [CONTRADICCION: [CONTRADICCION: 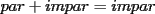 , y no par] , y no par] Saludos ^^ |
|
|
|
 May 16 2005, 03:40 AM May 16 2005, 03:40 AM
Publicado:
#7
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Felicidades...pero aun estoy esperando si son capaces de responder a los problemas siguientes:
P1)(Clasificación a la Olimpiada Nacional año 2001): En una ruleta circular se colocan los números del 1 al 36 al azar. Demuestre que necesariamente debe haber tres números consecutivos cuya suma sea al menos 55. Hint: trate de ver que es imposible que no haya tres números consecutivos cuya suma sea al menos 55, es decir, trate de probar que lo contrario nunca ocurre(demostración por contradicción). P2)(Clasificación a la Olimpíada Nacional año 2001): Juan nació antes del año 2000. El 25 de agosto del año 2001 cumple tantos años como es la suma de los dígitos del año de su nacimiento. Determine su fecha de nacimiento y justifique que es la única posible. P2*)Considere la ordenación de los primeros  números enteros positivos: números enteros positivos: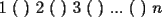 ¿Es posible colocar signos + o signos - dentro de cada ( ), de modo que al efectuar la operación resultante se obtenga 0 como resultado final? P3*)En un tablero cuadrado de lado par, se colocan fichas rectangulares de tamaño 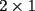 (fichas de dominó). Demuestre que si llenamos el tablero colocando fichas de modo que no me queden una sobre la otra, entonces el número de fichas dispuestas horizontalmente es par. (fichas de dominó). Demuestre que si llenamos el tablero colocando fichas de modo que no me queden una sobre la otra, entonces el número de fichas dispuestas horizontalmente es par.En resumen les falta contestar los dificiles..asi que como dije..espero sus creativas soluciones ^.^ -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
| Corecrasher |
 May 16 2005, 08:49 PM May 16 2005, 08:49 PM
Publicado:
#8
|
|
Invitado |
CITA(Kenshin @ May 16 2005, 04:40 AM) P2)(Clasificación a la Olimpíada Nacional año 2001): Juan nació antes del año 2000. El 25 de agosto del año 2001 cumple tantos años como es la suma de los dígitos del año de su nacimiento. Determine su fecha de nacimiento y justifique que es la única posible. Espero que este bien :S Por enunciado sabemos que el año de nacimiento debe ser 19_ _ (mil novecientos y algo), denotaremos  y y 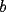 que son digitos que componen el numero de la siguiente manera : que son digitos que componen el numero de la siguiente manera : 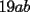 . .Sabemos que la edad que tenia el 2001 es el 2001 menos su AÑO de nacimiento: 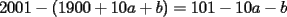 Tenemos que 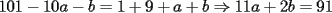 , pero , pero 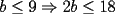 y por lo tanto y por lo tanto 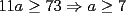 . Tambien, . Tambien, 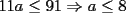 pero al ser pero al ser  y y 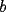 valores enteros tenemos que valores enteros tenemos que  puede ser 7, 8 (ya que son digitos), con puede ser 7, 8 (ya que son digitos), con 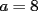 no sobra un numero par que puede ser representado por no sobra un numero par que puede ser representado por 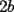 ( (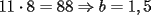 ), entonces no es solucion y por lo tanto la unica solucion es ), entonces no es solucion y por lo tanto la unica solucion es 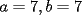 , teniendo finalmente que nacio el 25 de agosto de 1977 , teniendo finalmente que nacio el 25 de agosto de 1977Saludos ^^ |
|
|
|
 May 16 2005, 09:29 PM May 16 2005, 09:29 PM
Publicado:
#9
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 293 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 3 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Felicitaciones, ya esta la solucion para uno de los que faltaba. Aun quedan tres, asi que sigue con los otros. Recuerda, pon énfasis en tu redaccion.
Saludos Victor |
|
|
|
| Corecrasher |
 May 18 2005, 10:37 AM May 18 2005, 10:37 AM
Publicado:
#10
|
|
Invitado |
CITA(Kenshin @ May 16 2005, 04:40 AM) P3*)En un tablero cuadrado de lado par, se colocan fichas rectangulares de tamaño 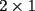 (fichas de dominó). Demuestre que si llenamos el tablero colocando fichas de modo que no me queden una sobre la otra, entonces el número de fichas dispuestas horizontalmente es par. (fichas de dominó). Demuestre que si llenamos el tablero colocando fichas de modo que no me queden una sobre la otra, entonces el número de fichas dispuestas horizontalmente es par.El problema radica en darnos cuenta de que cada vez que en un lado del cuadrado usamos un domino en forma vertical (dejando el lado 1 en el lado del cuadrado) debemos ocupar nuevamente una vertical para dejar el numero par ... ya que el otro lado mide 2 ... por lo tanto quedara un numero par de horizontales |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 13th July 2025 - 06:36 PM |








