|
|
|
|
|
|
|
  |
 May 18 2005, 03:45 PM May 18 2005, 03:45 PM
Publicado:
#11
|
|
|
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 167 Registrado: 17-May 05 Desde: Santiago, Chile Miembro Nº: 38 Nacionalidad:  Colegio/Liceo:  Sexo:  |
CITA(Kenshin @ May 16 2005, 04:40 AM) P2*)Considere la ordenación de los primeros  números enteros positivos: números enteros positivos: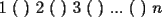 ¿Es posible colocar signos + o signos - dentro de cada ( ), de modo que al efectuar la operación resultante se obtenga 0 como resultado final? weno aka va: si es posible, siempre y cuando 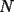 sea par,de ser asi si es posible, xq?? sea par,de ser asi si es posible, xq?? porque si es par se podra dividir en 2 y asi formar 2 grupos, uno + y el otro - , como: la forma mas facil es ir poniendo en los recuadros la siguiente combinacion de + y -: ![TEX: $[+--+]$](./tex/35161.gif) y asi repetida 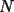 veces sea necesario veces sea necesarioweno eso bye --------------------  |
|
|
|
 May 18 2005, 08:30 PM May 18 2005, 08:30 PM
Publicado:
#12
|
|
 Matemático Grupo: Usuario FMAT Mensajes: 53 Registrado: 14-May 05 Desde: Santiago de Chile Miembro Nº: 24 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Hola Jaime.
Qué tal? Espero que bien. Bueno, talvez tú no me conoces, mi nombre es Pablo García y soy entrenador de los alumnos de enseñanza media de los SSCC. Respecto a P2*) me gustaría darte algunos consejos. Tu respuesta es correcta. Pero eso no es suficiente, cuando demuestres algo debes procurar ser claro y ordenado de manera que una persona con tus mismos conocimientos, que jamás se ha enfrentado a este problema pueda entender los argumentos que estás dando. En este problema estas evadiendo la columna vertebral de la problemática, debes hacer énfasis en explicar mejor todas aquellas cosas que puedan prestarse para dudas. Cuando te refieres a 2 grupos me imagino que estas hablando de 2 sumandos que son igual en numero, pero de distintos en signo, verdad? También sería interesante que en tu respuesta nos dijeras porque cuando 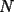 es impar no es posible obtener 0 como resultado. es impar no es posible obtener 0 como resultado.También es importante que sepas que encontrando una sola ordenación que hace posible que la suma sea 0 tendrás el problema resuelto, pues sólo te piden decidir si es “posible”, y si encontraste alguna forma de que se cumpla lo pedido, es claro que es posible. No es necesario que te arriesgues diciendo que alguna manera es más fácil que otra, pues tendríamos que explicar porque nuestra manera es más fácil que otras maneras. Espero que te sirvan estos consejitos. Ah! me gustaría que volvieras a postear una solución para el mismo problema, pero esta vez argumentando mejor, imagínate que le estas mostrando la solución a algunos de tus compañeros que no van a clases de Olimpiadas, ya? Una sugerencia, cuando redactes tu solución talvez te simplificaría algunas cosas utilizar la notación: 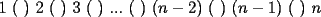 . .Yap mucha suerte y a trabajar, mira que cuando se conjugan suerte y conocimiento resultan cosas impredecibles, mucho éxito. Pablo. -------------------- Pablo García-|Estudiante de Licenciatura en matemáticas de la Pontificia Universidad Catolica de chile. Ramnujan series:  "He looks all over the genius he was."-Hardy |
|
|
|
 May 19 2005, 04:59 PM May 19 2005, 04:59 PM
Publicado:
#13
|
|
|
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 167 Registrado: 17-May 05 Desde: Santiago, Chile Miembro Nº: 38 Nacionalidad:  Colegio/Liceo:  Sexo:  |
ya da re lo mejor de mi pa ser claro en esto, (que me cuesta n poko
ya tenemos la combinacion: 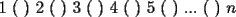 bueno mi respuesta es si , siempre y cuando 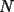 sea par y no sucede cuando sea par y no sucede cuando 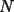 es impar. es impar.Par: 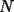 al ser par sera divisible por 2, teniendo asi: al ser par sera divisible por 2, teniendo asi: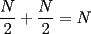 a un sumando, sea cual sea, se le cambia el signo a negativo, dejando uno positivo y otro negativo dara 0 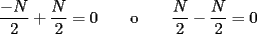 lo que demuestra que si 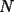 es par, se podra llegar a 0 es par, se podra llegar a 0Impar: en el impar, no se puede llegar a 0, ya que se estan buscando enteros que al restarse den 0, pero si se puede llegar a 1 o -1, puesto al no ser divisible x 2, no se podran conseguir 2 sumandos iguales lo que kiere decir que un sumando sera mayor al otro, hacinedo que a lo mas se pueda conseguir como resultado 1 o -1, dicese como expresion, en el mejor de los casos: 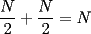 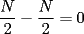 entonces si se suma 1 o resta 1 a la ecuacion para que 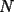 sea par quedaria sea par quedaria lo que respalda que si 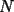 es impar el resultado sera a lo mas 1 es impar el resultado sera a lo mas 1weno eso ojala te bn chauZ salu2 --------------------  |
|
|
|
 May 20 2005, 02:57 AM May 20 2005, 02:57 AM
Publicado:
#14
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Muy bien..ya estas explicando mucho mejor pero hago enfasis en algunos detallitos...
1)(Minimo) En el problema hay una  minuscula y despues una minuscula y despues una 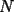 mayuscula..la idea es que uses siempre la misma letra(por estetica mayuscula..la idea es que uses siempre la misma letra(por estetica 2)Tu dices que si  es par funciona, y si consideramos es par funciona, y si consideramos 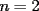 altiro no funciona :? altiro no funciona :? 3)Si  es impar el resultado es "a lo mas 1" :!: , seguro?..si yo tengo el 1,2,3 ( es impar el resultado es "a lo mas 1" :!: , seguro?..si yo tengo el 1,2,3 (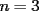 ) y los pongo como 1+2+3=6 me dio mas que 1. A que apunto con esto?...que quizas lo que tu piensas no es lo mismo que esta escrito en el post(o en el papel..en el caso de una olimpiada)...tienes que transcribir lo que piensas al papel...y tener mucho cuidado con las afirmaciones que haces...(o sea si en el papel dice que el resultado es a lo mas 1,la persona que lo lea...entendera que "el resultado es a lo mas 1"...jejeje) ) y los pongo como 1+2+3=6 me dio mas que 1. A que apunto con esto?...que quizas lo que tu piensas no es lo mismo que esta escrito en el post(o en el papel..en el caso de una olimpiada)...tienes que transcribir lo que piensas al papel...y tener mucho cuidado con las afirmaciones que haces...(o sea si en el papel dice que el resultado es a lo mas 1,la persona que lo lea...entendera que "el resultado es a lo mas 1"...jejeje)4)El hecho de que  sea par y lo puedas dividir en 2 no implica nada en particular..o sea no quiere decir que haya una configuracion en la cual una parte sume la mitad...y la otra parte la otra mitad(no se si me explique bien,pero si en el cole me dices quien eres gustoso te doy un ejemplo para aclararte esa idea) sea par y lo puedas dividir en 2 no implica nada en particular..o sea no quiere decir que haya una configuracion en la cual una parte sume la mitad...y la otra parte la otra mitad(no se si me explique bien,pero si en el cole me dices quien eres gustoso te doy un ejemplo para aclararte esa idea)Bueno...eso seria por ahora...saludos ^.^ PD:Y sigue posteando..el objetivo de este foro es que todos aprendan...los que postean muy bien sus soluciones ahora,al principio tuvieron los mismos dramas que tu..asi que sigue adelante...este es solo el comienzo... -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
| Corecrasher |
 Aug 10 2005, 05:48 PM Aug 10 2005, 05:48 PM
Publicado:
#15
|
|
Invitado |
CITA(Kenshin @ May 16 2005, 04:40 AM) P1) En una ruleta circular se colocan los números del 1 al 36 al azar. Demuestre que necesariamente debe haber tres números consecutivos cuya suma sea al menos 55. Bueno hoy me dio por revisar de pe a pa el foro y me encontre con este que me gusto arto... asi que aca va la sol: Sean 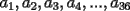 los numeros en la ruleta que van del 1 al 36 sin repetirse , pensemos que nunca hay 3 numeritos consecutivos que al menos suman 55 , ordenando: los numeros en la ruleta que van del 1 al 36 sin repetirse , pensemos que nunca hay 3 numeritos consecutivos que al menos suman 55 , ordenando: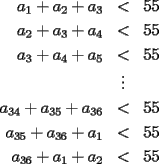 Sumando las desigualdades tenemos en el lado izquierdo 3 veces la suma de todas las aes y la suma de 1 a 36 es 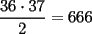 1998<1980 , la contradicción prueba lo pedido |
|
|
|
 Dec 23 2005, 10:23 PM Dec 23 2005, 10:23 PM
Publicado:
#16
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 414 Registrado: 19-May 05 Desde: puente alto, santiago Miembro Nº: 45 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Esta solucion tambien correcta, es un buen metodo probar por contradiccion.
bien explicada y te felicito por  esima vez jajajaj esima vez jajajajFrancisco Muñoz Espinoza Ahora tan solo falta el problema propuesto por xsebastian : Se dispone de 1999 bolitas numeradas del 1 al 1999. Encontrar todos los enteros positivos 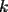 con la siguiente propiedad: el total de bolitas se puede separar en con la siguiente propiedad: el total de bolitas se puede separar en 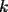 grupos, de modo que la suma de los números de las bolitas en cada uno de los grupos sea la misma. grupos, de modo que la suma de los números de las bolitas en cada uno de los grupos sea la misma.
-------------------- "No tenemos la solucion a todos los problemas del mundo en nuestras manos... Pero frente a los problemas del mundo tenemos nuestras manos..."
Teresa de Calcuta |
|
|
|
 Feb 18 2006, 09:36 PM Feb 18 2006, 09:36 PM
Publicado:
#17
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
CITA(nico @ May 13 2005, 05:41 AM) P2*)Considere la ordenación de los primeros  números enteros positivos: números enteros positivos: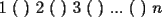 ¿Es posible colocar signos + o signos - dentro de cada ( ), de modo que al efectuar la operación resultante se obtenga 0 como resultado final? P3*)En un tablero cuadrado de lado par, se colocan fichas rectangulares de tamaño 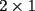 (fichas de dominó). Demuestre que si llenamos el tablero colocando fichas de modo que no me queden una sobre la otra, entonces el número de fichas dispuestas horizontalmente es par. (fichas de dominó). Demuestre que si llenamos el tablero colocando fichas de modo que no me queden una sobre la otra, entonces el número de fichas dispuestas horizontalmente es par.CITA(xsebastian @ May 14 2005, 04:57 PM) Se dispone de 1999 bolitas numeradas del 1 al 1999. Encontrar todos los enteros positivos Estos son los problemas pendientes de solución hasta ahora, en este rincón del foro. Tres problemas que, debo decir, no son tan complicados como parece en un comienzo. Por algo están al nivel de séptimos y octavos básicos. Me decidí a rescatarlos, porque veía tan poca actividad en este lugar, desde hace algún tiempo con la siguiente propiedad: el total de bolitas se puede separar en con la siguiente propiedad: el total de bolitas se puede separar en 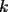 grupos, de modo que la suma de los números de las bolitas en cada uno de los grupos sea la misma. grupos, de modo que la suma de los números de las bolitas en cada uno de los grupos sea la misma.En el problema P2*) había una solución de Jaime sscc que no está correcta, según veredicto de Kenshin. El problema P3*) tiene una solucion propuesta por Corecrasher, que no me convence, o sea está mal explicada, o definitivamente mala. Veamos lo que escribió: CITA(Corecrasher @ May 18 2005, 12:37 PM) El problema radica en darnos cuenta de que cada vez que en un lado del cuadrado usamos un domino en forma vertical (dejando el lado 1 en el lado del cuadrado) debemos ocupar nuevamente una vertical para dejar el numero par ... ya que el otro lado mide 2 ... por lo tanto quedara un numero par de horizontales Una cosa es que los lados no tienen por qué medir 2, como crítica aparte, no entiendo bien lo que quiere decir. O sea, necesitamos una solución mejor explicada.Para este problema manejo dos soluciones, si bien no he chequeado si se trata de lo mismo. Pongan su mejor entusiasmo para finiquitar este tema... Salu -------------------- |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 18th September 2025 - 01:41 PM |











