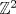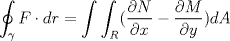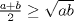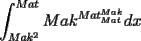|
|
|
|
|
|
|
  |
 Aug 23 2008, 08:03 PM Aug 23 2008, 08:03 PM
Publicado:
#1
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 836 Registrado: 9-January 07 Desde: Santiasko Miembro Nº: 3.659 Nacionalidad:  Sexo:  |
20ª OLIMPIADA NACIONAL DE MATEMÁTICAS Prueba de Clasificación, Nivel Menor Primera Prueba Problema 1: Se tienen  naranjas apiladas en una piramide triangular. ¿Cuántas naranjas hay en la base de la pirámide? naranjas apiladas en una piramide triangular. ¿Cuántas naranjas hay en la base de la pirámide?Problema 2: En cada lado de un cuadrado de lado 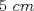 se marcan cuatro puntos de modo de subdividir cada lado en cinco partes iguales, y se unen como en la figura. ¿Cuál es el area de la región achurada? se marcan cuatro puntos de modo de subdividir cada lado en cinco partes iguales, y se unen como en la figura. ¿Cuál es el area de la región achurada? Problema 3: El conjunto 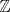 de los números enteros es dividido en de los números enteros es dividido en  partes (disjuntas) y no vacías partes (disjuntas) y no vacías 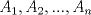 que verifican la siguiente propiedad: si que verifican la siguiente propiedad: si  y y  pertenecen a pertenecen a 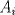 entonces su suma entonces su suma  pertenece al mismo conjunto pertenece al mismo conjunto 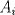 . Determine los posibles valores del entero positivo . Determine los posibles valores del entero positivo  . .Segunda Prueba Problema 4: Encuentre todos los enteros positivos 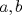 tales que tales que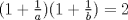 Problema 5: Se tiene un triángulo rectángulo de catetos 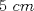 y y 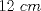 . Con centro en cada cateto se construye una circunferencia que pasa por el vértice del ángulo recto y es tangente a la hipotenusa (vea la figura). Calcule la razón entre los radios de ambas circunferencias. . Con centro en cada cateto se construye una circunferencia que pasa por el vértice del ángulo recto y es tangente a la hipotenusa (vea la figura). Calcule la razón entre los radios de ambas circunferencias. Problema 6: En cada casilla de un tablero de 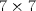 hay una ampolleta. Además, se cuenta con hay una ampolleta. Además, se cuenta con 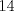 interruptores. Para cada fila existe un interruptor que, al ser presionado, cambia el estado de las ampolletas de dicha fila (las que estaban encendidas se apagan, y las que estaban apagadas se encienden). Para cada columna se cuenta también con un interruptor que cambia el estado de las ampolletas en ella. Usando estos interruptores, ¿es siempre posible llegar, a partir de cualquier estado inicial, a un estado en el cual el número de ampolletas encendidas en cada fila o columna es interruptores. Para cada fila existe un interruptor que, al ser presionado, cambia el estado de las ampolletas de dicha fila (las que estaban encendidas se apagan, y las que estaban apagadas se encienden). Para cada columna se cuenta también con un interruptor que cambia el estado de las ampolletas en ella. Usando estos interruptores, ¿es siempre posible llegar, a partir de cualquier estado inicial, a un estado en el cual el número de ampolletas encendidas en cada fila o columna es 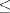 al de ampolletas apagadas de dicha fila o columna? al de ampolletas apagadas de dicha fila o columna?
|
|
|
|
 Aug 23 2008, 08:19 PM Aug 23 2008, 08:19 PM
Publicado:
#2
|
|
 Matemático Grupo: Usuario FMAT Mensajes: 55 Registrado: 3-May 06 Desde: Location Unknow Miembro Nº: 1.018 Nacionalidad:  Universidad:  Sexo:  |
QUOTE El conjunto 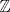 de los números enteros es dividido en de los números enteros es dividido en  partes (disjuntas) y no vacías partes (disjuntas) y no vacías 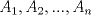 que verifican la siguiente propiedad si que verifican la siguiente propiedad si  y y  pertenecen a pertenecen a 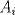 entonces su suma entonces su suma  pertenece al mismo conjunto pertenece al mismo conjunto 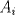 . Determine los posibles valores del entero positivo . Determine los posibles valores del entero positivo  . .nvm .me condorie =O! Mensaje modificado por hect0r el Aug 23 2008, 08:29 PM -------------------- "Dios creo los números naturales, todo lo demás es obra del hombre"
Leopold Kronecker Estudiante de Matemagica , de por vida Curriculum : |
|
|
|
 Aug 23 2008, 08:26 PM Aug 23 2008, 08:26 PM
Publicado:
#3
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 836 Registrado: 9-January 07 Desde: Santiasko Miembro Nº: 3.659 Nacionalidad:  Sexo:  |
|
|
|
|
 Aug 23 2008, 08:27 PM Aug 23 2008, 08:27 PM
Publicado:
#4
|
|
|
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 171 Registrado: 13-May 07 Desde: Viña del Mar Miembro Nº: 5.820 Nacionalidad:  Colegio/Liceo:  Sexo:  |
-------------------- Saludos
 "El secreto de la felicidad no es hacer siempre lo que se quiere sino querer siempre lo que se hace" Tolstoi |
|
|
|
 Aug 23 2008, 08:42 PM Aug 23 2008, 08:42 PM
Publicado:
#5
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 836 Registrado: 9-January 07 Desde: Santiasko Miembro Nº: 3.659 Nacionalidad:  Sexo:  |
P4
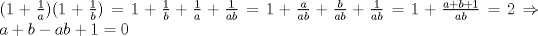 . . Restamos 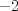 y tenemos y tenemos 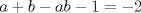 , pero , pero 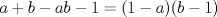 , reemplazando: , reemplazando: 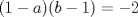 , como , como 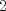 es primo entonces existen dos unicas posibles representaciones como producto de dos factores enteros para es primo entonces existen dos unicas posibles representaciones como producto de dos factores enteros para 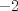 : : 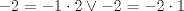 . Entonces hay 4 casos: . Entonces hay 4 casos:Caso 1: 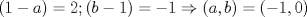 , pero , pero 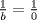 se indefine, por tanto no nos sirve este caso. se indefine, por tanto no nos sirve este caso.Caso 2: 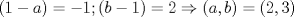 , este par si cumple con la relacion inicial. , este par si cumple con la relacion inicial.Caso 3: 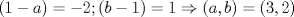 , par que cumple. , par que cumple.Caso 4: 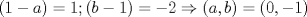 que no satisface pues 1/a no se define. que no satisface pues 1/a no se define.Las unicas parejas posibles son 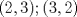 EDITADO: minimo error de tipeo... Mensaje modificado por Felipe_ambuli el Aug 23 2008, 10:14 PM |
|
|
|
 Aug 23 2008, 09:38 PM Aug 23 2008, 09:38 PM
Publicado:
#6
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 836 Registrado: 9-January 07 Desde: Santiasko Miembro Nº: 3.659 Nacionalidad:  Sexo:  |
P2
 Lo que hacemos aqui es pintar ciertas zonas del cuadrado inicial. Se pintan los "bordes" de colores celeste, esmeralda (creo), naranjo y rojo. Lo que hacemos a continuacion es pegar la parte esmeralda junto a la naranja, quedando un triangulo verde. De la misma forma se pega el celeste sobre el rojo quedando un azul. El area de la figura conseguida es  , al area del cuadrado original, pues lo unico que hicimos fue trasladar areas /y formamos finalmente la figura que esta encerrada en una linea negra). Ahora bien, esta area se divide en 26 cuadraditos, entonces el area de lo achurado (que en el fondo es cada cuadradito) es , al area del cuadrado original, pues lo unico que hicimos fue trasladar areas /y formamos finalmente la figura que esta encerrada en una linea negra). Ahora bien, esta area se divide en 26 cuadraditos, entonces el area de lo achurado (que en el fondo es cada cuadradito) es 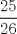 . .
|
|
|
|
 Aug 23 2008, 10:08 PM Aug 23 2008, 10:08 PM
Publicado:
#7
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 836 Registrado: 9-January 07 Desde: Santiasko Miembro Nº: 3.659 Nacionalidad:  Sexo:  |
|
|
|
|
 Aug 24 2008, 09:40 PM Aug 24 2008, 09:40 PM
Publicado:
#8
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 143 Registrado: 6-February 08 Desde: desde aquí Miembro Nº: 15.300 Nacionalidad:  Colegio/Liceo:  Sexo:  |
yo el problema 2 lo respondí de una forma muy rara xDD dije "si cada
![TEX: \[<br />\sqrt {26} <br />\]<br />](./tex/25e4966ee4810d6424e69ce3aae1b582.png) entonces en la linea del medio podriamos decir que ambos segmentos que no son iguales a los otros, son iguales entre ellos podriamos decir que los 4 segmentos restantes que son iguales serían entonces en la linea del medio podriamos decir que ambos segmentos que no son iguales a los otros, son iguales entre ellos podriamos decir que los 4 segmentos restantes que son iguales serían ![TEX: \[<br />\sqrt {26} - 2x<br />\]](./tex/f318e8068292b7e31f733b836669fa97.png) y bueno luego hice algo (que no me puedo acordar que era xD sabes que aca lo estoy intentando denuevo pero no recuerdo como lo hice) para despejar x y luego alfinal me dio los y bueno luego hice algo (que no me puedo acordar que era xD sabes que aca lo estoy intentando denuevo pero no recuerdo como lo hice) para despejar x y luego alfinal me dio los ![TEX: \[<br />\frac{{25}}<br />{{26}}<br />\]<br />](./tex/afa46ab71a55ff6d5f95e54901adabfa.png)
-------------------- |Ente Inmiscible|  |
|
|
|
 Aug 25 2008, 11:40 PM Aug 25 2008, 11:40 PM
Publicado:
#9
|
|
 Dios Matemático Supremo Grupo: Moderador Mensajes: 590 Registrado: 14-October 07 Miembro Nº: 11.310 Colegio/Liceo:  Universidad:  Sexo:  |
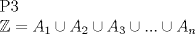 Se nos pide hallar los  posibles en los que se divide posibles en los que se divide 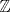 , pero con la condición de que , pero con la condición de que{ 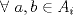 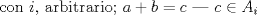 } }Osea cada 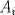 presentan la propiedad de cierre o clausura con respecto a la Suma. presentan la propiedad de cierre o clausura con respecto a la Suma.Luego considerando dos subconjuntos consecutivos 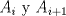 , definidos como , definidos como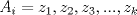 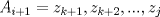 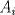 y y 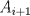 no presentan elementos en común (son disjuntos) luego sea no presentan elementos en común (son disjuntos) luego sea 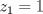 , sumando este elemento a otro del mismo conjunto, tenemos , sumando este elemento a otro del mismo conjunto, tenemos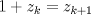 , osea un elemento que no pertenece a , osea un elemento que no pertenece a 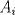 , sino al subconjunto siguiente, de esto se concluye que los subconjuntos deben tener infinitos elementos tal que contengan la suma de cualquiera de dos de sus elementos. , sino al subconjunto siguiente, de esto se concluye que los subconjuntos deben tener infinitos elementos tal que contengan la suma de cualquiera de dos de sus elementos.Se sabe que 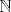 presenta la propiedad de cierre o clausura en la Suma, y además presenta la propiedad de cierre o clausura en la Suma, y además 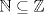 , análogamente para , análogamente para 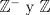 (también son cerrados en la adición), conclusión los (también son cerrados en la adición), conclusión los  posibles son: 1, porque posibles son: 1, porque 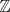 cumple con las condiciones del enunciado; 2 dado por los subconjuntos cumple con las condiciones del enunciado; 2 dado por los subconjuntos 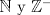 (notar que el (notar que el  puede estar en los enteros negativos o en los Naturales, por ser elemento neutro no afecta las condiciones); y 3, dado por los subconjuntos nombrados anteriormente en el 2 pero considerando al puede estar en los enteros negativos o en los Naturales, por ser elemento neutro no afecta las condiciones); y 3, dado por los subconjuntos nombrados anteriormente en el 2 pero considerando al  como un subconjunto aparte ya que también es cerrado en Suma. como un subconjunto aparte ya que también es cerrado en Suma.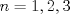 Espero se entienda vale por tu solucion felipe master xdd al P4(yo lo hice buscando numeros perfectos aqui esta la solucion al P3 espero este buena. -------------------- |
|
|
|
 Sep 14 2008, 02:31 PM Sep 14 2008, 02:31 PM
Publicado:
#10
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 836 Registrado: 9-January 07 Desde: Santiasko Miembro Nº: 3.659 Nacionalidad:  Sexo:  |
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 17th June 2025 - 05:45 PM |