|
|
|
|
|
|
|
  |
 Aug 23 2008, 08:21 PM Aug 23 2008, 08:21 PM
Publicado:
#1
|
|
 Coordinador General Gran Maraton PSU Final 2008 Grupo: Moderador Mensajes: 1.607 Registrado: 11-June 07 Desde: Peñalolen, Stgo Miembro Nº: 6.641 Nacionalidad:  Universidad:  Sexo:  |
20ª OLIMPIADA NACIONAL DE MATEMÁTICAS Prueba de Clasificación, Nivel Mayor Primera Prueba Problema 1. Se tienen 680 naranjas apiladas en una pirámide triangular. ¿Cuantas naranjas hay en la base de la pirámide? Problema 2. En cada lado de un cuadrado de lado  se marcan se marcan 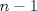 puntos de modo de subdividir cada lado en n partes iguales, y se unen como en la figura. ¿Cual es el área de la región achurada? puntos de modo de subdividir cada lado en n partes iguales, y se unen como en la figura. ¿Cual es el área de la región achurada?Problema 3. El conjunto ![TEX: \[<br />\mathbb{Z}^2 <br />\]](./tex/cdd05cac38fdfd58a5080e911d962102.png) es dividido en es dividido en  partes (disjuntas) y no vacías partes (disjuntas) y no vacías ![TEX: \[<br />A_1 ,...,A_n <br />\]<br />](./tex/e16fb407c6c2bc312ee738ff48fb3521.png) que verifican la siguiente propiedad: si que verifican la siguiente propiedad: si  y y  pertenecen a pertenecen a ![TEX: \[<br />A_i <br />\]](./tex/5c7fd68f20f29c518d0cd56508159ffe.png) entonces su suma entonces su suma  pertenece al mismo conjunto pertenece al mismo conjunto ![TEX: \[<br />A_i <br />\]](./tex/8a6c8823c0b3978716eb01be3aebae12.png) . Determine los posibles valores del entero positivo n. . Determine los posibles valores del entero positivo n.Observacion: recuerde que la suma de ![TEX: \[<br />a = \left( {m,n} \right) \in \mathbb{Z}^2 <br />\]](./tex/bc2b5341e0e5076305dc20401847bd12.png) y y ![TEX: \[<br />b = \left( {m',n'} \right) \in \mathbb{Z}^2 <br />\]](./tex/d02022212f105ce0af1d209a4a08d798.png) es definida como es definida como ![TEX: \[<br />\left( {m + m',n + n'} \right)<br />\]<br />](./tex/d7c2c6e3609f20eb0cae71a5e7b941cb.png) Segunda Prueba Problema 4. Se definen las sucesiones ![TEX: \[<br />x_n <br />\]](./tex/b73b8eab1c73443744a7af6cb21a7cb5.png) , , ![TEX: \[<br />y_n <br />\]<br />](./tex/c40d01eb187fad961c9f0dbf3077c601.png) mediante las siguientes reglas mediante las siguientes reglas ![TEX: \[<br />x_0 = 2<br />\]](./tex/2d6593d91358bf1059aac32fe52380fd.png) , , ![TEX: \[<br />x_1 = 5<br />\]<br />](./tex/04bdcf32468732e2932a121c4bb4a9f1.png) , , ![TEX: \[<br />x_{n + 1} = x_n + 2x_{n - 1} <br />\]<br /><br />](./tex/d15c62aa6d65b1b09fae26432a9bb76f.png) , , ![TEX: \[<br />y_0 = 3<br />\]<br />](./tex/358225d99d987aa34e8678d06d4ddb2c.png) , , ![TEX: \[<br />y_1 = 4<br />\]<br />](./tex/57347d4eeea9409843287c2fcd980828.png) , , ![TEX: \[<br />y_{n + 1} = y_n + 2y_{n - 1} <br />\]<br />](./tex/ff2fc575f24c535de48c4f770db12e8b.png) . Pruebe que los conjuntos . Pruebe que los conjuntos ![TEX: \[<br />\left\{ {x_n :n \geqslant 0} \right\}<br />\]](./tex/46ac180729caa8ff37e4f1e1a4bf2db9.png) y y ![TEX: \[<br />\left\{ {y_n :n \geqslant 0} \right\}<br />\]<br />](./tex/92fd6db02bffbb2b33dd8f3a66547e8e.png) son disjuntos. son disjuntos.Problema 5. Se tienen dos circunferencias ![TEX: \[<br />C_1 <br />\]](./tex/ee39ead8ea2e9da190483a7b6ae45004.png) y y ![TEX: \[<br />C_2 <br />\]<br />](./tex/0283a9eaf2f22ff8baaf5714652c899a.png) tangentes (externamente) entre sí y tangentes a una recta tangentes (externamente) entre sí y tangentes a una recta 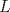 (por el mismo lado). Desde el punto P de mayor altura (respecto a (por el mismo lado). Desde el punto P de mayor altura (respecto a 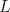 ) en ) en ![TEX: \[<br />C_1 <br />\]](./tex/298797cbbe3d5f2699466e945a0c02d5.png) se traza la tangente "superior" se traza la tangente "superior" 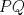 a a ![TEX: \[<br />C_2 <br />\]<br />](./tex/fe1c3dd55c49258041ff95b0005c3932.png) : vea la figura. Pruebe que la longitud de : vea la figura. Pruebe que la longitud de 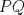 es igual al diametro de es igual al diametro de ![TEX: \[<br />C_1 <br />\]<br />](./tex/eec026dc0c926850b73fa44bd4133273.png) Problema 6. En cada casilla de un tablero ![TEX: \[<br />n \times n<br />\]<br />](./tex/5b3efd56565d26249c94e38b71cbe960.png) se tiene una ampolleta. Ademas, se cuenta con se tiene una ampolleta. Ademas, se cuenta con 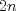 interruptores. Para cada fila existe un interruptor que, al ser presionado, cambia el estado de las ampolletas de dicha fila (las que estaban encendidas se apagan, y las que estan apagadas se encienden). Para cada columna se cuenta tambien con un interruptor que cambia el estado de las ampolletas en ella. Usando estos interruptores, ¿es siempre posible llegar, a partir de cualquier estado inicial, a un estado en el cual el numero de ampolletas encendidas en cada fila o columna es menor o igual al de ampolletas apagadas en dicha fila o columna? interruptores. Para cada fila existe un interruptor que, al ser presionado, cambia el estado de las ampolletas de dicha fila (las que estaban encendidas se apagan, y las que estan apagadas se encienden). Para cada columna se cuenta tambien con un interruptor que cambia el estado de las ampolletas en ella. Usando estos interruptores, ¿es siempre posible llegar, a partir de cualquier estado inicial, a un estado en el cual el numero de ampolletas encendidas en cada fila o columna es menor o igual al de ampolletas apagadas en dicha fila o columna?
--------------------  |
|
|
|
 Aug 23 2008, 09:12 PM Aug 23 2008, 09:12 PM
Publicado:
#2
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Problema 4. Se definen las sucesiones ![TEX: \[<br />x_n <br />\]](./tex/b73b8eab1c73443744a7af6cb21a7cb5.png) , , ![TEX: \[<br />y_n <br />\]<br />](./tex/c40d01eb187fad961c9f0dbf3077c601.png) mediante las siguientes reglas mediante las siguientes reglas ![TEX: \[<br />x_0 = 2<br />\]](./tex/2d6593d91358bf1059aac32fe52380fd.png) , , ![TEX: \[<br />x_1 = 5<br />\]<br />](./tex/04bdcf32468732e2932a121c4bb4a9f1.png) , , ![TEX: \[<br />x_{n + 1} = x_n + 2x_{n - 1} <br />\]<br /><br />](./tex/d15c62aa6d65b1b09fae26432a9bb76f.png) , , ![TEX: \[<br />y_0 = 3<br />\]<br />](./tex/358225d99d987aa34e8678d06d4ddb2c.png) , , ![TEX: \[<br />y_1 = 4<br />\]<br />](./tex/57347d4eeea9409843287c2fcd980828.png) , , ![TEX: \[<br />y_{n + 1} = y_n + 2y_{n - 1} <br />\]<br />](./tex/ff2fc575f24c535de48c4f770db12e8b.png) . Pruebe que los conjuntos . Pruebe que los conjuntos ![TEX: \[<br />\left\{ {x_n :n \geqslant 0} \right\}<br />\]](./tex/46ac180729caa8ff37e4f1e1a4bf2db9.png) y y ![TEX: \[<br />\left\{ {y_n :n \geqslant 0} \right\}<br />\]<br />](./tex/92fd6db02bffbb2b33dd8f3a66547e8e.png) son disjuntos. son disjuntos.Solución al problema 4  Saludos. -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
 Aug 23 2008, 09:35 PM Aug 23 2008, 09:35 PM
Publicado:
#3
|
|
 Coordinador General Gran Maraton PSU Final 2008 Grupo: Moderador Mensajes: 1.607 Registrado: 11-June 07 Desde: Peñalolen, Stgo Miembro Nº: 6.641 Nacionalidad:  Universidad:  Sexo:  |
P5
Denotemos como es usual con 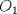 y y 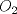 a los centros de la circunferencias y como a los centros de la circunferencias y como 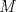 y y 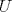 las tangencias de las tangencias de 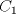 y y 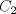 a a 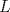 respectivamente. Sean respectivamente. Sean 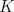 y y 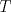 las proyecciones ortogonales de las proyecciones ortogonales de 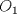 y y 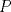 sobre sobre 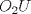 . . Dibujo.PNG ( 23.51k )
Número de descargas: 9
Dibujo.PNG ( 23.51k )
Número de descargas: 9La mayor altura sobre 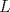 corresponde al diametro de corresponde al diametro de 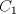 que llamaremos que llamaremos 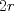 . Es decir . Es decir  y y 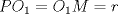 . .Siendo 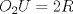 , por Pitagoras tenemos: , por Pitagoras tenemos:![TEX: \[<br />\left( {O_1 O_2 } \right)^2 - \left( {O_2 T} \right)^2 = \left( {O_1 T} \right)^2 \Rightarrow \left( {R + r} \right)^2 - \left( {R - r} \right)^2 = \left( {O_1 T} \right)^2 \Rightarrow 2\sqrt {Rr} = O_1 T<br />\]<br />](./tex/6eb59ed19523445c7075d672c9d1e4de.png) Luego notamos que ![TEX: \[<br />O_1 T = PK<br />\]<br />](./tex/9b45f4de6b5b1429e5877ba3327e82e5.png) por ser perpendiculares a por ser perpendiculares a 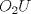 Nuevamente por Pitagoras: ![TEX: \[<br />\left( {O_2 K} \right)^2 + \left( {PK} \right)^2 = \left( {O_2 P} \right)^2 \Rightarrow \left( {R - 2r} \right)^2 + \left( {2\sqrt {Rr} } \right)^2 = \left( {O_2 P} \right)^2 \Rightarrow \sqrt {4r^2 + R^2 } = O_2 P<br />\]<br />](./tex/7b244b707cf236725a83b109cc90c388.png) Finalmente, usando otra vez Pitagoras obtenemos: ![TEX: \[<br />\left( {O_2 P} \right)^2 - \left( {O_2 Q} \right)^2 = \left( {QP} \right)^2 \Rightarrow \left( {\sqrt {4r^2 + R^2 } } \right)^2 - \left( R \right)^2 = \left( {QP} \right)^2 \Rightarrow QP = 2r<br />\]](./tex/3f84dc2d2083bbefce854c5612b99809.png) Demostrando lo pedido. --------------------  |
|
|
|
 Aug 23 2008, 09:41 PM Aug 23 2008, 09:41 PM
Publicado:
#4
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Problema 1. Se tienen 680 naranjas apiladas en una pirámide triangular. ¿Cuantas naranjas hay en la base de la pirámide? Solución al problema 1   Saludos. -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
 Aug 23 2008, 09:44 PM Aug 23 2008, 09:44 PM
Publicado:
#5
|
|
 Coordinador General Gran Maraton PSU Final 2008 Grupo: Moderador Mensajes: 1.607 Registrado: 11-June 07 Desde: Peñalolen, Stgo Miembro Nº: 6.641 Nacionalidad:  Universidad:  Sexo:  |
eee lo hice igual --------------------  |
|
|
|
 Aug 23 2008, 09:47 PM Aug 23 2008, 09:47 PM
Publicado:
#6
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 878 Registrado: 14-May 07 Desde: Talcahuano Miembro Nº: 5.845 Nacionalidad:  Colegio/Liceo:  Sexo:  |
 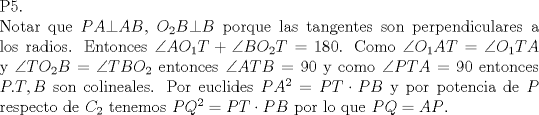
Mensaje modificado por pelao_malo el Aug 23 2008, 10:57 PM --------------------  |
|
|
|
 Aug 23 2008, 09:49 PM Aug 23 2008, 09:49 PM
Publicado:
#7
|
|
|
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 171 Registrado: 13-May 07 Desde: Viña del Mar Miembro Nº: 5.820 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Cuándo dicen los resultados?
-------------------- Saludos
 "El secreto de la felicidad no es hacer siempre lo que se quiere sino querer siempre lo que se hace" Tolstoi |
|
|
|
 Aug 23 2008, 09:51 PM Aug 23 2008, 09:51 PM
Publicado:
#8
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Cuándo dicen los resultados? Falta muuuuuuuuuuuuuuuuuuuuuuuuuuuuuuucho xD Problema 6. En cada casilla de un tablero ![TEX: \[<br />n \times n<br />\]<br />](./tex/5b3efd56565d26249c94e38b71cbe960.png) se tiene una ampolleta. Ademas, se cuenta con se tiene una ampolleta. Ademas, se cuenta con 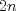 interruptores. Para cada fila existe un interruptor que, al ser presionado, cambia el estado de las ampolletas de dicha fila (las que estaban encendidas se apagan, y las que estan apagadas se encienden). Para cada columna se cuenta tambien con un interruptor que cambia el estado de las ampolletas en ella. Usando estos interruptores, ¿es siempre posible llegar, a partir de cualquier estado inicial, a un estado en el cual el numero de ampolletas encendidas en cada fila o columna es menor o igual al de ampolletas apagadas en dicha fila o columna? interruptores. Para cada fila existe un interruptor que, al ser presionado, cambia el estado de las ampolletas de dicha fila (las que estaban encendidas se apagan, y las que estan apagadas se encienden). Para cada columna se cuenta tambien con un interruptor que cambia el estado de las ampolletas en ella. Usando estos interruptores, ¿es siempre posible llegar, a partir de cualquier estado inicial, a un estado en el cual el numero de ampolletas encendidas en cada fila o columna es menor o igual al de ampolletas apagadas en dicha fila o columna?Algunos Hints para la que podria ser la Pregunta mas simpatica de esta Clasificación.
La Pregunta 3 tambien la encontre interesante En resumen, una Clasificación mas simple de lo acostumbrado, entretenida, y motivante para los que estan participando por 1era vez, en lo que hoy en dia es La Olimpiada mas Importante del Pais. Mis Saludos -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Aug 23 2008, 09:52 PM Aug 23 2008, 09:52 PM
Publicado:
#9
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 836 Registrado: 9-January 07 Desde: Santiasko Miembro Nº: 3.659 Nacionalidad:  Sexo:  |
CITA 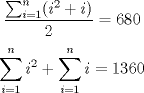 *** no se me ocurrio, lo deje hasta ahi no mas, mas me falto tiempo |
|
|
|
 Aug 23 2008, 09:54 PM Aug 23 2008, 09:54 PM
Publicado:
#10
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
 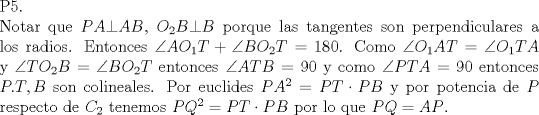 Saludos -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 16th June 2025 - 08:30 AM |











