Prueba de Clasificación - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Sector Preparación Olimpiadas > Competencias y Olimpiadas > Olimpiadas > Olimpiada Nacional

9 Páginas:

« < 3 4 5 6 7 > »

Reply to this topic

Start new topic

Prueba de Clasificación, Nivel Mayor (2008)

pato foncea Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 24 2008, 05:12 PM Publicado: #41
Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 20 Registrado: 18-July 08 Miembro Nº: 30.198 Nacionalidad: Sexo:	en la priemra prueba hice los dos primeros pero no explique ocm llegue al resltado en el primero, y en el segndo remplze n por 5... el ttercero podia ser 9?? es que una miga me dijo que le dio 4, porque considero eso mismo de los plaos cartesianos (+,+), (+,-),(-,+),(-,-), peor yo creo qye tambien pueden haber los conjuntos de (0,0),(0,+),(0,-),(-,0) y(+,0), supongo

pelao_malo Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 24 2008, 05:59 PM Publicado: #42
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 878 Registrado: 14-May 07 Desde: Talcahuano Miembro Nº: 5.845 Nacionalidad: Colegio/Liceo: Sexo:	$TEX: \noindent Notar que $$x_n=\frac{7\cdot 2^n-(-1)^n}{3}$$ $$y_n=\frac{7\cdot 2^n+2\cdot (-1)^n}{3}$$ Si para alg\'un par $(i,j)$ tuvi\'eramos $x_i=y_j$ entonces $$7\cdot 2^i+(-1)^i=7\cdot 2^j+2\cdot (-1)^j$$ que en m\'odulo $7$ se vuelve $$(-1)^i\equiv 2\cdot (-1)^j(7)$$ pero ninguna de las congruencias $$-1\equiv 2(7)$$ $$-1\equiv -2(7)$$ $$1\equiv 2(7)$$ $$1\equiv -2(7)$$ es cierta por lo que no existen dichos $(i,j)$...$ Mensaje modificado por pelao_malo el Aug 24 2008, 06:07 PM -------------------- $TEX: $\sqrt{5}=41$$

supermantematico Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 24 2008, 06:02 PM Publicado: #43
Principiante Matemático Grupo: Usuario FMAT Mensajes: 3 Registrado: 12-May 07 Desde: Chillán Miembro Nº: 5.804 Nacionalidad: Sexo:	A mi también me fué mas o menos, creo tener el p1 y el p4 aunque fue un poco curioso como saque el p1, pero igual me dió aunque en una parte debí poner (n+2) en vez de (n+1), en el p2 me pasó algo similar y puse (n-1)^2 en vez de n^2+1 Y el p6 no alcanzé a explicarlo bien. Te apoyo pelao, ojalá nos tengan piedad, aunque dudo que con lo poco que alcanzé a hacer quede en la selección. Saludos.

Soul_Hunter Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 24 2008, 09:25 PM Publicado: #44
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 665 Registrado: 12-June 07 Desde: the city of the fallen angels Miembro Nº: 6.649 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(Killua @ Aug 23 2008, 09:02 PM) Solución al problema 4 $TEX: \noindent Veamos que $x_0=2, x_1=5, x_2=9, x_3=19, \ldots$. Como $x_{n+1}=x_n+2x_{n-1}\Rightarrow{x_{n+1}-x_n}=2x_{n-1}$, por lo que $x_{n+1}$ y $x_n$ tienen la misma paridad, con $n\ge{1}$ (la recurrencia se define desde $n=1$). Por lo tanto $x_j$ siempre es impar, con $j\ge{1}$.\\<br /><br />\noindent Veamos que $y_0=3, y_1=4, y_2=10, y_3=18, \ldots$. Como $y_{n+1}=y_n+2y_{n-1}\Rightarrow{y_{n+1}-y_n}=2y_{n-1}$, por lo que $y_{n+1}$ y $y_n$ tienen la misma paridad, con $n\ge{1}$ (la recurrencia se define desde $n=1$). Por lo tanto $y_k$ es siempre impar, con $k\ge{1}$.\\<br /><br />\noindent De este modo, los $x_j$ son impares, con $j\ge{1}$, y los $y_k$ son pares $(k\ge{1})$; y ya que $x_0\neq{y_0}$, los conjuntos $\{x_n:n\ge{0}\}$ y $\{y_n:n\ge{0}\}$ no tienen elementos en com\'un, como se ped\'ia $\blacksquare$$ Saludos. El p4 lo resolví así, un poco menos justificado, pero la idea es la misma. xD CITA(Killua @ Aug 23 2008, 09:31 PM) Solución al problema 1 $TEX: \noindent En la cumbre de la pir\'amide (capa $1$), hay una naranja, en la siguiente capa (capa $2$) hay $1+2=3$ naranjas, en la tercera capa hay $1+2+3=6$ naranjas, $\ldots$, en la capa $n$ hay $1+2+3+\ldots+n=\frac{n(n+1)}{2}$ naranjas. Esto ya que cada capa es un tri\'angulo formado por naranjas, es decir, la capa $n$ est\'a formada por el en\'esimo n\'umero triangular (de la forma $\frac{n(n+1)}{2}$).\\<br /><br />\noindent As\'i, si la pir\'amide de $680$ naranjas tiene $n$ capas, tenemos lo siguiente:<br /><br />$$\displaystyle\sum_{i=1}^{n}\frac{i(i+1)}{2}=680$$<br />$$\displaystyle\frac{\sum_{i=1}^{n}(i^2+i)}{2}=680$$<br />$$\displaystyle{\sum_{i=1}^{n}i^2}+\displaystyle\sum_{i=1}^{n}i=1360$$<br />$$\displaystyle{\frac{n(n+1)(2n+1)}{6}+\frac{n(n+1)}{2}}=1360$$<br />$$n^3+3n^2+2n-4080=0$$<br />$$\boxed{(n-15)(n^2+18n+272)=0}\ (i)$$$ $TEX: \noindent Entonces $n_1=15$ es una ra\'iz de la ecuaci\'on $(i)$; descartamos las otras ra\'ices, pues claramente son complejas. As\'i, tenemos que $n=15$, y en esta capa, que corresponde a la base de la pir\'amide, hay $\frac{15\cdot{16}}{2}=120$ naranjas $\blacksquare$$ Saludos. Ídem, salvo que la ecuación cúbica la resolví igual que CyedqD. En cuanto leí el problema supe que tenía que aplicar sumatorias. CITA(Rurouni Kenshin @ Aug 24 2008, 12:59 PM) En la PUC tambien dieron hora y media por etapa, ¿estas seguro que en Conce fueron 2 horas? (en todas las sedes se deberia haber dado el mismo tiempo). Como vi gente de otros lados ellos nos podrian comentar cuanto tiempo se les dio (o sea hoy en dia nada se puede hacer, pues ya esta hecho, pero al menos se puede evitar esos detalles de coordinacion que a la hora de clasificar igual influyen). Sí, en Conce fueron 2 horas en ambas pruebas Resumen: p1: bastante bueno xD p2: también bueno, pero no justifiqué tanto como pelao malo p3: pude haberlo tenido bueno, porque pensé en el plano cartesiano así que puse n=2 y n=4, pero no sabía si un conjunto podía tener un solo elemento o si podía tenerlos todos, así que descarté cualquier opción que me dejara al (0,0) como un conjunto aparte ; aparte que me faltó tiempo. p4: bueno, pero poco justificado p5: asumí algo que no debí, así que no llegué a nada. Me lo eché muy rico... p6: ni lo intenté resolver, perdí demasiado tiempo en el p5, así que sólo escribí algo para no dejar la hoja en blanco. Ojalá que clasifique... también quiero jugar maffia de nuevo xD, me fue mejor que el año pasado así que aún no pierdo las esperanzas. Salu2 --------------------

JoNy_SaTiE Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 25 2008, 05:01 PM Publicado: #45
Dios Matemático Supremo Grupo: Colaborador Gold Mensajes: 1.118 Registrado: 11-September 05 Desde: Valdivia/Ancud Miembro Nº: 302 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(Killua @ Aug 23 2008, 09:02 PM) $TEX: \noindent Por lo tanto $y_k$ es siempre impar$ Hay un error de tipeo, $TEX: $y_k$ es par.$ -------------------- Comienza a crear documentos con LaTeX. Ya usas LaTeX y quieres aprender un poco más ... pincha aquí Si eres de la UaCH ... únete a la causa !!! J. Jonathan H. Oberreuter A. Universidad Austral de Chile - RWTH Aachen alumni Est. Magister en Acústica y Vibraciones Ingeniero Civil Acústico (E) Bachiller y Licenciado en Cs. de la Ingeniería

Killua Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 25 2008, 08:05 PM Publicado: #46
Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(JoNy_SaTiE @ Aug 25 2008, 05:52 PM) Hay un error de tipeo, 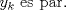$TEX: $y_k$ es par.$ Gracias, error editado. Es que copié lo mismo de arriba y después cambié las x por y xD, y me faltó poner par en lugar de impar. Saludos -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy) "A mathematician is a device for turning coffee into theorems" (Paul Erdös)

Gaston Burrull	Aug 30 2008, 12:35 AM Publicado: #47
Invitado	Yo primera vez que voy a una olimpiada. La primera la resolvi con la funcion cúbica, gracias a que pensé en sumatorias . La 4 pensando en pares e impares. En la 2 puse area = 1 . La hize muy rápido. En la 3 contesté que eran infinitas soluciones, demostré que todas las rectas que pasaban por el origen cumplían la condición del problema, no sé si la tenga buena. La 5 me complicó bastante, de una manera realmente extraña llegué a una semejanza de triángulos para la demostración. Hize tantas líneas que me enredé bastante u.u. En la 6, puse que siempre se puede llegar a tal configuración, explicandolo en muy pocas lineas. Espero clasificar... creo que solamente tengo la 1 y la 4 totalmente buenas.

unknown Ver Perfil del Miembro Ver los mensajes de este miembro	Sep 9 2008, 05:26 PM Publicado: #48
Dios Matemático Grupo: Usuario FMAT Mensajes: 220 Registrado: 17-October 06 Desde: Mi casa (al fin tngo wifi! :D) Miembro Nº: 2.558 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	p1:facil,pero olvide indicar que solo servia n=15 P2:facil,solobastaba uasr Euclides P3:no pude P4:tampoco P5:menos(COMO NO SE ME OCURRIO!!!!!!!) P6:aca va es obvio en el caso n=1 con n=2: XO OX cumple la condicion, X esta apagado, 1 sola ampolleta encendida cumple con tres, habra una fila o columna encendida completa, bastara apagarla para tener una sola encendida. entonces use induccion supongamos que puedo hacerlo para un tablero de nn y le agrego una columna y una fila, obteninendo un tablero de (n+1)(n+1). si se da que una columna tenga mas encendidas que apagadas, basta encenderlas todas, con los interruptores de las filas, luego apagarlas todas con el interruptor de la columna y encender finalmente las que estaban apagadas al principio, que son menos que las que van a quedar apagadas. Semejante razonamiento en las filas. con ello pruebo p(n)=>p(n+1) QED toy apurado luego la expilco mejor Mensaje modificado por unknown* el Sep 11 2008, 06:13 PM -------------------- El 98% de los adolescentes han fumado, si eres del dichoso 2% que no lo ha hecho, copia y pega esto en tu firma "Es súper fácil cuando tienes la solución al frente" Claudio Lobos. "A veces el sesgo ideológico bloquea el razonamiento aritmético" Patricio Meller. "You could try to code the game and then complain to me" Greg McLeod "Es que lo nuestro es utópico" Ruby Hidalgo R. "¡Chúpate esa, negro!" Leonardo "Tata" Sánchez. "El 90% de las cosas ocurren porque sí" José Manuel "Manolo" Aguilera "Te van a patear" Patricia Godoy Álvarez "Bienvenidos a Beauchef" Fabián Bravo "Se nos murió el paciente" Marcelo "Lasaña" "La-Hazaña" Leseigneur "Querer ganar un partido de tenis no prueba que seas Kira" L "(insert word here) the cosine" Randall Munroe (xkcd.com) "El unknown es especial pero con cuatica" egadoobkn "No importa, te quiero por como eres (L)" El Geek "Y si queres pasarla mal, dividí con decimal" Yayo, Cumbia matemática. "El mérito es de Chopin, yo solo soy un mero... le titul." Carlos Nuñez Cortés (Les Luthiers) "'Los que hoy son niños, mañana serán hombres.' ¡Qué manera abrupta de crecer!" Daniel Rabinovich (Les Luthiers) Voy a resolver este propuesto... -what's this? NO WOLFRAM NO GEOGEBRA NO BOOKS LATEX ONLY FINAL DESTINATION

cacovp Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 4 2008, 09:28 PM Publicado: #49
Principiante Matemático Grupo: Usuario FMAT Mensajes: 1 Registrado: 4-October 08 Miembro Nº: 35.342 Nacionalidad: Sexo:	hola soy nuevo por aca, me fue mas o menos en la prueba, pero tengo una duda, si el primer ejercicio lo resolvi probando todos los numeros del 1 al 15 hasta llegar a la respuesta como esta el ejercicio bien, mal o medio.

Rurouni Kenshin Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 4 2008, 09:36 PM Publicado: #50
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad: Sexo:	CITA(cacovp @ Oct 4 2008, 09:18 PM) hola soy nuevo por aca, me fue mas o menos en la prueba, pero tengo una duda, si el primer ejercicio lo resolvi probando todos los numeros del 1 al 15 hasta llegar a la respuesta como esta el ejercicio bien, mal o medio. Si, yo pienso que esta completamente bien (dado que al seguir probando con otros números mas grandes nos pasaríamos del valor pedido, concordamos que no debería haber mas soluciones al problema, asi que quizás no por el método mas elegante, pero si matemáticamente valido, deberías tener todo el puntaje de la pregunta). Segun fuentes confiables, los resultados deberian estar pronto (o sea las pruebas ya estan revisadas y solo se afinan algunos detalles para proceder a publicar los clasificados a este magno evento). Estos resultados se publican en la Web Oficial de la Olimpiada de Matematicas (deberian ponerla en favoritos de su navegador) http://www.olimpiadadematematica.cl/ Mucha suerte a todos PD: Y revivió FMAT -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!) Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)

« Posterior · Olimpiada Nacional · Anterior »

9 Páginas:

« < 3 4 5 6 7 > »

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 16th June 2025 - 11:32 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.