|
|
|
|
|
|
|
  |
 Aug 26 2006, 07:27 PM Aug 26 2006, 07:27 PM
Publicado:
#1
|
|
 Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 25 Registrado: 19-August 05 Desde: santiago chile Miembro Nº: 255 Nacionalidad:  Sexo:  |
18ª OLIMPIADA NACIONAL DE MATEMÁTICAS Prueba de Clasificación, Nivel Menor Primera Prueba Problema 1: Sean 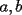 numeros reales distintos tales que numeros reales distintos tales que 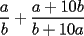 . Encuentre . Encuentre 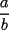 . .Problema 2: El vertice 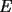 de un cuadrado de un cuadrado 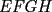 de lado 2006 mm se encuntra en el centro del cuadrado de lado 2006 mm se encuntra en el centro del cuadrado 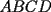 de lado 10 mm. El trazo de lado 10 mm. El trazo 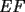 intersecta a intersecta a 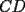 en el punto en el punto 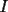 . El trazo . El trazo 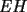 intercepta a intercepta a 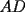 en en 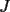 . Si . Si 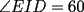 . Calcule el area del cuadrilatero . Calcule el area del cuadrilatero 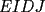 . .Problema 3: El numero 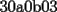 en notacion decimal es divisible por 13. Encuentre los posibles valores de los digitos en notacion decimal es divisible por 13. Encuentre los posibles valores de los digitos 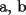 . .Segunda Prueba Problema 4: En un tablero rectangular de 2006 casillas, distribuidas en 34 filas y 59 columnas, seran colocados tres botones identicos en el centro de las casillas determinando un triangulo. ¿ de cuantas menras distintas podemos colocar los botones formando un triangulo ractangulo con catetos paralelos a los bordes del tablero? Problema 5: Sea 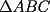 un triángulo cualquiera y un triángulo cualquiera y 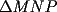 el triángulo formado por los puntos de tangencia del círculo inscrito con los lados del triangulo el triángulo formado por los puntos de tangencia del círculo inscrito con los lados del triangulo 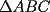 , demostrar que si , demostrar que si 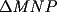 es equilatero, entonces el es equilatero, entonces el 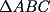 es equlatero. es equlatero.Problema 6: Un numero natural se llama palíndromo, Cuando se obtiene el mismo numero al escribir sus digitos en orden inverso, por ejemplo 23432 ; 565 ; 8 son palíndromos. determine todos los pares enteros positivos 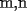 tales que tales que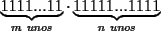 , es palíndromo. , es palíndromo.
-------------------- Por aqui paso Tygger
 SS.CC Fco Garrido |
|
|
|
 Aug 26 2006, 08:14 PM Aug 26 2006, 08:14 PM
Publicado:
#2
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 209 Registrado: 12-June 05 Desde: Sagrados Corazones Alameda Miembro Nº: 98 Nacionalidad:  Sexo:  |
PROBLEMA 3
El numero 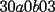 puede ser escrito de la siguiente forma: puede ser escrito de la siguiente forma: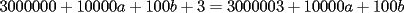 Aplicaremos congruencia en modulo 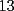 , de esta forma: , de esta forma: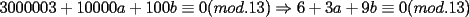 Esto implica que : 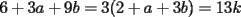 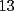 es primo, por lo que debe dividir a uno de los dos factores, es claro que es primo, por lo que debe dividir a uno de los dos factores, es claro que 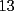 no divide a no divide a  , por lo que necesariamente , por lo que necesariamente 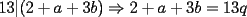 El maximo valor de la expresion 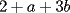 , se alcanza cuando , se alcanza cuando 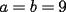 y toma el valor de y toma el valor de 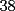 . Luego hay que encontrar todos los . Luego hay que encontrar todos los 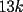 , tal que , tal que 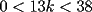 , esto implica que , esto implica que 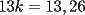 Luego basta ponerse en ambos casos: Caso 1: 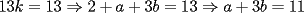 Si 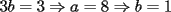 . Si . Si  . Si . Si 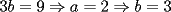 Luego tenemos que: 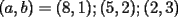 Caso 2: 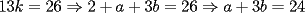 Encontraremos las soluciones pensando en que 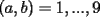 , y esto se consigue cuando , y esto se consigue cuando 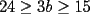 Si 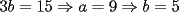 . Si . Si 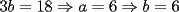 . Si . Si 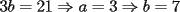 . Si . Si 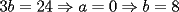 Luego tenemos que: 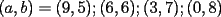 .................................................................................................... ...................... En conclusion, los valores son: 
-------------------- SS - CC , SS - CC , SS - CC , SAGRADOS CORAZONES DE ALAMEDA!!
T_TNIVERSIDAD DE CHILE GRACIAS POR EXISTIR!!! VAMOS LOS LEONES!!! |
|
|
|
 Aug 26 2006, 08:36 PM Aug 26 2006, 08:36 PM
Publicado:
#3
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
  screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img245.imageshack.us/img245/5020/p5pm5.png');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img245.imageshack.us/img245/5020/p5pm5.png');}" /> Salu 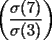 Mensaje modificado por Killua el Aug 26 2006, 10:09 PM -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
 Aug 26 2006, 08:44 PM Aug 26 2006, 08:44 PM
Publicado:
#4
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
CITA(ZeuS @ Aug 26 2006, 09:14 PM) PROBLEMA 3 El numero 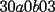 puede ser escrito de la siguiente forma: puede ser escrito de la siguiente forma: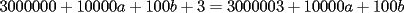 Aplicaremos congruencia en modulo 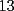 , de esta forma: , de esta forma: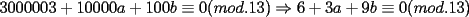 Esto implica que : 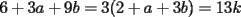 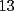 es primo, por lo que debe dividir a uno de los dos factores, es claro que es primo, por lo que debe dividir a uno de los dos factores, es claro que 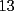 no divide a no divide a  , por lo que necesariamente , por lo que necesariamente 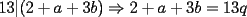 El maximo valor de la expresion 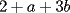 , se alcanza cuando , se alcanza cuando 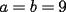 y toma el valor de y toma el valor de 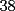 . Luego hay que encontrar todos los 13k, tal que . Luego hay que encontrar todos los 13k, tal que 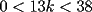 , esto implica que , esto implica que 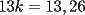 Luego basta ponerse en ambos casos: Caso 1: 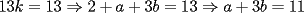 Si 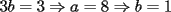 . Si . Si  . Si . Si 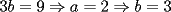 Luego tenemos que: 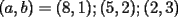 Caso 2: 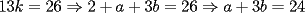 Encontraremos las soluciones pensando en que 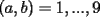 , y esto se consigue cuando , y esto se consigue cuando 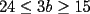 Si 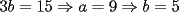 . Si . Si 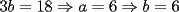 . Si . Si 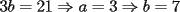 . Si . Si 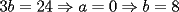 Luego tenemos que: 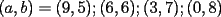 .................................................................................................... ...................... En conclusion, los valores son:  A mi juicio, este era el problema que discriminaba en esta Clasificacion Nacional Felicitaciones -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Aug 26 2006, 09:05 PM Aug 26 2006, 09:05 PM
Publicado:
#5
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 209 Registrado: 12-June 05 Desde: Sagrados Corazones Alameda Miembro Nº: 98 Nacionalidad:  Sexo:  |
Si
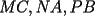 fueran biscetrices, estarias asumiendo que fueran biscetrices, estarias asumiendo que 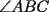 , es equilatero. , es equilatero.
-------------------- SS - CC , SS - CC , SS - CC , SAGRADOS CORAZONES DE ALAMEDA!!
T_TNIVERSIDAD DE CHILE GRACIAS POR EXISTIR!!! VAMOS LOS LEONES!!! |
|
|
|
 Aug 26 2006, 09:08 PM Aug 26 2006, 09:08 PM
Publicado:
#6
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
CITA(ZeuS @ Aug 26 2006, 10:05 PM) Saludos -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
 Aug 26 2006, 09:11 PM Aug 26 2006, 09:11 PM
Publicado:
#7
|
|
 Dios Matemático Supremo Grupo: Colaborador Silver Mensajes: 725 Registrado: 17-July 05 Desde: Puente Alto-Santiago Miembro Nº: 148 Nacionalidad:  Universidad:  Sexo:  |
[Yupi] El problemilla 1 tiene su historia.
Luego de haber ido a jugar pool con emilio (Animiko) (para no frustrarnos luego de salir de la clasificatoria nacional) venia de vuelta en la micro, y me acorde de este problema. La gracia está en que lo hize con una """""""bella"""""" o.O musica de fondo, 3 "hip-hoperos" venian cantando y rayando la micro al lado mio Desarrollo: Sea ![TEX: \[<br />\dfrac{a}{b} = x \Longrightarrow a = bx<br />\]<br />](./tex/113512.gif) reemplazamos en la ecuación y tenemos: reemplazamos en la ecuación y tenemos:![TEX: \[<br />\begin{array}{l}<br /> x + \dfrac{{bx + 10b}}{{b + 10bx}} = 2 \\ <br /> \\ <br /> \Rightarrow x + \dfrac{{x + 10}}{{1 + 10x}} = 2 \\ <br /> \\ <br /> \Rightarrow x + 10x^2 + x + 10 = 2 + 20x \\ <br /> \\ <br /> \Rightarrow 5x^2 - 9x + 4 = 0 \\ <br /> \end{array}<br />\]<br />](./tex/113513.gif) Buscando las soluciones a la ecuación ![TEX: <br />\[<br />\begin{array}{l}<br /> 5x^2 - 9x + 4 = 0/*5 \\ <br /> (5x)^2 - 9(5x) + 20 = 0 \\ <br /> (5x - 4)(5x - 5) = 0/ \div 5 \\ <br /> (5x - 4)(x - 1) = 0 \\ <br /> \end{array}<br />\]](./tex/113514.gif) Por lo tanto el cunjunto solución es: ![TEX: \[<br />x = \left\{ {\dfrac{4}{5},1} \right\}<br />\]](./tex/113515.gif) Pero como el enunciado afirma que ![TEX: \[<br />\begin{array}{l}<br /> a \ne b \\ <br /> \\ <br /> \Rightarrow \frac{a}{b} \ne 1 \\ <br /> \end{array}<br />\]](./tex/113516.gif) La solución al problema es solo que : ![TEX: \[<br />\dfrac{a}{b} = \dfrac{4}{5}<br />\]<br />](./tex/113517.gif) q.e.d Saludos -------------------- "Resolver un problema es una meta específica de la inteligencia e inteligencia es el don específico de los seres humanos: Resolver un problema es la actividad humana por excelencia"
  |
|
|
|
 Aug 27 2006, 01:03 AM Aug 27 2006, 01:03 AM
Publicado:
#8
|
|
 Matemático Grupo: Usuario FMAT Mensajes: 57 Registrado: 22-April 06 Desde: ? Miembro Nº: 922 |
oe, caxaste que todos salian de la prueba altiro?. Casi siempre los que quedabamos de los ultimos eramos nosotros(Oratorio) y ustedes(IN)...A, y no caxe q onda ese compadre que decia: "me puedo sentar en la punta"?,o sea,era demasiado formal,= ta bn...
Taba muy dificl no? ME fue remal, y eso que deberia haberme ido bien por la edad,sera, bye -------------------- ¡¡El talento no discrimina lugar de nacimiento ni condicion social!! Jonas Valdivieso
|
|
|
|
 Aug 27 2006, 10:09 AM Aug 27 2006, 10:09 AM
Publicado:
#9
|
|
 Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 25 Registrado: 19-August 05 Desde: santiago chile Miembro Nº: 255 Nacionalidad:  Sexo:  |
Aqui va la solucion al problema 2
 screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img169.imageshack.us/img169/5783/nacional1ul7.png');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img169.imageshack.us/img169/5783/nacional1ul7.png');}" />notemos en la figura los triangulos ICE y JED Primero demonos cuenta que los trazos DE y EC son iguales ya que son semi diagonales del cuadrado ABCD. luego miremos el angulo EDJ con ECI que tambien son iguales en 45º ya que los parten las diagonales del cuadrado. Finalmente veamos IED que vale 15º ya que si nos fijamos en el triangulo DEI, tiene sus angulo 45 y 60 por lo tanto el otro deve valer 15. Por otro lado notemos queel angulo EIC vale 120, por lo tanto el angulo IEC vale 15 por el mismo criterio anterior. por esto se ca pr conclusion que los triangulos DEJ y EIC sn congruentes por criterio ALA. Ahora como esos dos triangulos son congruentes lel cuadrado ABCD lo podemos rotar de la sigiente forma sin que el cuadrilatero DJEI varia su area.  screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img228.imageshack.us/img228/4529/nacional2ul4.png');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img228.imageshack.us/img228/4529/nacional2ul4.png');}" />partamonos dandonos cuenta del triangulo DAB para calcular la diagonal del cuadrado ABCD de lado 10 ( por pitagoras) 10^2 + 10^2 = X^2 200= X^2 X=10√2 pero como nosotros nesecitamos los lados DE y EC que son iguales y ademas es la mitad de la diagonal del cuadrado ABCD. Se tiene el triangulo rectangulo DEC ( isoceles de lados 5√2) por lo tanto ahora calcularemos el area de este triangulo que es base por altura partido en 2. 5√2^2 = 25 * 2 = 50 luego dividimos en 2. 50/2= 25 por lo tanto el area del triangulo DEC es 25 mm^2 que es la misma area a la del cuadrilatero EIDJ. finalmente Area cuadrilatero EIDJ = 25 mm^2 saludos -------------------- Por aqui paso Tygger
 SS.CC Fco Garrido |
|
|
|
 Aug 27 2006, 10:34 AM Aug 27 2006, 10:34 AM
Publicado:
#10
|
|
 Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 25 Registrado: 19-August 05 Desde: santiago chile Miembro Nº: 255 Nacionalidad:  Sexo:  |
esta es otra solucion al problema 5
vamos a comenzar asumiendo que el triangulo MNP es equilatero  screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img174.imageshack.us/img174/7682/nacional3ew5.png');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img174.imageshack.us/img174/7682/nacional3ew5.png');}" />notemos que en la figura los angulos PMN, NPM, MNP valen 60º por lo tanto los arcos MP, MN y NP son iguales y valen 120 como estos tres arcos son iguales los angulos que estan sostenidos tambien son iguales. estos son ACB, BAC y CBA y como los angulos interiores de un triangulo suman 180 y los tres de eelos son iguales 3x = 180 x=60 por lo tanto el triangulo ABC tambien es equilatero -------------------- Por aqui paso Tygger
 SS.CC Fco Garrido |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 13th May 2025 - 04:35 AM |












 , es equilatero.
, es equilatero.