|
|
|
|
|
|
|
  |
 Aug 27 2006, 11:57 AM Aug 27 2006, 11:57 AM
Publicado:
#11
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
CITA(mahuachi @ Aug 27 2006, 02:03 AM) oe, caxaste que todos salian de la prueba altiro?. Casi siempre los que quedabamos de los ultimos eramos nosotros(Oratorio) y ustedes(IN)...A, y no caxe q onda ese compadre que decia: "me puedo sentar en la punta"?,o sea,era demasiado formal,= ta bn... Taba muy dificl no? ME fue remal, y eso que deberia haberme ido bien por la edad,sera, bye [jugo] si, ese tipo era súper enfermo xD "para qué entregan tres hojas?" xD "que hago ahora?" xD. Y con respecto a los que salieron de la prueba, no duraron ni 5 minutos ¬¬ ( y uno ahí cabeceándose por clasificar Saludos -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
 Aug 27 2006, 12:23 PM Aug 27 2006, 12:23 PM
Publicado:
#12
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 178 Registrado: 28-May 05 Desde: Aca , alla , aca , alla Miembro Nº: 70 Nacionalidad:  Universidad:  Sexo:  |
Y q hago ahora!!!
Y puedo ir al baño!!! haha lo mejor del dia...!!! pobre lco... yo no me podia reir porq taba tomando la prueba xD pero muy chistoso Y QUE HAGO AHORA? el prox de nuevo DEBO ir a tomar pruebas! pa verlo d nuevo jajajaj -------------------- Por un lado la matematica , lo mas importante , pero por el otro el basquetbol y ginobili lo mejor q hay!!!!
Team Naranja!!! Apagando incendios xD    |
|
|
|
 Aug 27 2006, 12:27 PM Aug 27 2006, 12:27 PM
Publicado:
#13
|
|
 Matemático Grupo: Usuario FMAT Mensajes: 57 Registrado: 22-April 06 Desde: ? Miembro Nº: 922 |
jaja, son malos...
jaja, pero igual era gil...berp... -------------------- ¡¡El talento no discrimina lugar de nacimiento ni condicion social!! Jonas Valdivieso
|
|
|
|
 Aug 27 2006, 03:57 PM Aug 27 2006, 03:57 PM
Publicado:
#14
|
|
 Matemático Grupo: Usuario FMAT Mensajes: 32 Registrado: 30-April 06 Desde: Puente Asko! Miembro Nº: 997 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Uhhh taba curioso el problema 6!
Bueno, no me pregunten por qué, pero en algun momento de ocio en el colegio, me di cuenta k si multiplicacbay cualkier nu con puros unos, siempre era lo mismo que para atrás k paraa delante Adelante prueben , entonces esa respoues debería ser Para todos los m y n que pertenezcan a los naturales Si hubiera que demostrar... yo cre k habria k ponerse a jugar tcon las sumas cuando uno multiplica y llegar a algo más serio -------------------- SE HACEN ESTAMPADOS... CUALQUIER CONSULTA MANDAR MENSAJE
|
|
|
|
 Aug 27 2006, 06:30 PM Aug 27 2006, 06:30 PM
Publicado:
#15
|
|
|
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 167 Registrado: 17-May 05 Desde: Santiago, Chile Miembro Nº: 38 Nacionalidad:  Colegio/Liceo:  Sexo:  |
CITA Ivan Acrata Escrito el Hoy, 04:57 PM Uhhh taba curioso el problema 6! Bueno, no me pregunten por qué, pero en algun momento de ocio en el colegio, me di cuenta k si multiplicacbay cualkier nu con puros unos, siempre era lo mismo que para atrás k paraa delante Adelante prueben , entonces esa respoues debería ser Para todos los m y n que pertenezcan a los naturales Si hubiera que demostrar... yo cre k habria k ponerse a jugar tcon las sumas cuando uno multiplica y llegar a algo más serio emmm.. estas equivocado, no dare la respuesta a este problema, pero simplemente te digo que veas cuando M y N son ambos mayores o igual que 10 por ejemplo con M=N=10 obtienes el numero: 1234567900987654321 el cual no es un capicua (o palindonoseke) weno Para aportar algo, dare mi respuesta el P4, que era muy simple..  screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img243.imageshack.us/img243/4295/trianguloth3.jpg');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img243.imageshack.us/img243/4295/trianguloth3.jpg');}" />solo hacia darse cuenta lo siguiente: Como todos sabemos, las distancia desde la interseccion de dos tangentes a los dos puntos de tangencia es igual, por ende los 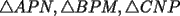 son Isoceles. son Isoceles.Luego notamos que : 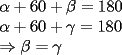 Luego 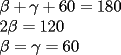 De aqui concluimos que el 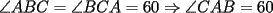 , por ende el , por ende el  es Equilatero es Equilaterosalu2 --------------------  |
|
|
|
 Aug 27 2006, 08:16 PM Aug 27 2006, 08:16 PM
Publicado:
#16
|
|
 Matemático Grupo: Usuario FMAT Mensajes: 57 Registrado: 22-April 06 Desde: ? Miembro Nº: 922 |
oigan, en el 6 yo puse algo que decia que eran infinitos pares, y que la unica restiriccion que tenian estas multiplicaciones parano ser palindromas era que m y n fueran = o mayor a 10. Si m y n no son = o mayores que 10, cualquier otra multiplicacion es palindroma....Por ej, 1*11 es palindromo y asi, con m=1 podemos multiplicr por n=infinitos 1 y = seria palindromo...
-------------------- ¡¡El talento no discrimina lugar de nacimiento ni condicion social!! Jonas Valdivieso
|
|
|
|
 Sep 7 2006, 12:45 AM Sep 7 2006, 12:45 AM
Publicado:
#17
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
  Salu ( -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
| Cesarator |
 Oct 6 2006, 07:59 PM Oct 6 2006, 07:59 PM
Publicado:
#18
|
|
Invitado |
|
|
|
|
 Oct 6 2006, 10:12 PM Oct 6 2006, 10:12 PM
Publicado:
#19
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
CITA(Cesarator @ Oct 6 2006, 08:59 PM) Veamos... trataré de explicarme mejor, pero creo que el argumento se entiende...  Saludos -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
| Cesarator |
 Oct 6 2006, 11:10 PM Oct 6 2006, 11:10 PM
Publicado:
#20
|
|
Invitado |
... a que te refieres con "bot'on de referencia"?
Advierto que, asi como esta, una correccion rigurosa descontaria puntos. Por ejemplo, dados dos botones en fila, para formar un triangulo rectangulo hay mas de 58 casillas posibles para el tercer boton... |
|
|
|
  |
2 usuario(s) está(n) leyendo esta discusión (2 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 13th May 2025 - 04:39 AM |












