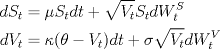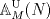I3 Álgebra Abstracta - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa Enseñanza Universitaria > Comunidades Universitarias > Universidad Católica > Álgebra Abstracta

Reply to this topic

Start new topic

I3 Álgebra Abstracta, 1-2009

DressedToKill Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 27 2009, 12:26 AM Publicado: #1
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.818 Registrado: 21-December 06 Miembro Nº: 3.434	Acá va la I3 del primer semestre del 2009, prof. Ángel Carocca. $TEX: \noindent<br /><br />\begin{center}\bf{INTERROGACION III\\<br />MAT2205 - ALGEBRA ABSTRACTA I }\end{center}<br /><br /><br />\begin{enumerate}<br />\item Sea $p$ un número primo. Para $m=a+b \sqrt{p} \in D = \mathbb{Z}[\sqrt{p}]$, se define <br />$$N(m) = \|a^2-pb^2\|$$<br />Pruebe las siguientes afirmaciones:<br />\begin{enumerate}<br />\item Para cada $n,m \in D$ se tiene <br />$$N(nm)=N(n)N(m)$$ <br />\item $m$ es invertible en $D$ si y sólo si $N(m) = 1$ ($m$ es invertible si existe $m^{-1}$ $\quad$ en $D$). <br />\item $\mathbb{Z}[\sqrt2]$ tiene infinitos elementos invertibles.<br />\end{enumerate}<br /><br />\item Sea $R$ un anillo con $1 \in R$. Sea $e \in R - \{0\}$ tal que $e^2=e$. \\<br />Considere<br />$$R_1 = \{xe / x \in R\}$$<br />\begin{enumerate}<br />\item Pruebe que $R_1$ es subanillo de $R$. <br />\item Construya un subanillo $R_2$ de $R$ tal que $R = R_1 \oplus R_2$, eso es $R_1 \cap R_2 = \{0\}$ y para cada $x \in R$ existen únicos $x_i \in R_i$ tales que $x = x_1 + x_2$.<br />\end{enumerate}<br /><br />\item Sea $p$ un número primo. Considere la función<br />$$\Phi : \mathbb{Z}[x] \rightarrow \mathbb{Z}_p[x]$$<br />tal que $f(x) = \displaystyle\sum_{i=0}^n a_i x^i \rightarrow \Phi (f(x)) = \displaystyle\sum_{i=0}^n \overline{a}_i x^i = \overline{f(x)}$.<br /><br />\begin{enumerate}<br />\item Pruebe que $\Phi$ es un epimorfismo.<br />\item Sea $f(x)$ un polinomio mónico en $\mathbb{Z}[x]$. Pruebe que si $\overline{f(x)}$ es irreducible en $\mathbb{Z}_p$, entonces $f(x)$ es irreducible en $\mathbb{Q}$.<br />\item Pruebe que $f(x) = x^4+10x^3+15x^2+5x+12$ es irreducible sobre $\mathbb{Q}$.<br /><br />\end{enumerate}<br /><br />\end{enumerate}<br /><br />$ Algunos comentarios. En la pregunta 1, $TEX: $\mathbb{Z}[\sqrt{p}] = \{a + \sqrt{p} \cdot b / a,b \in \mathbb{Z} \}$$ . En la pregunta 2, 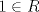$TEX: $1 \in R$$ indica que el anillo tiene unidad y $TEX: $0$$ hace referencia al neutro de la "suma" en el anillo. En la pregunta 3, 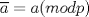$TEX: $\overline{a} = a (modp)$$ . Esta prueba no estaba tan dificil, el 1.c es el más interesante. Ojalá alguien se anime con soluciones, sino pongo algunas mias -------------------- http://www.youtube.com/watch?v=sp_WV91jx8E...feature=related

Gaston Burrull	Jul 27 2009, 02:12 AM Publicado: #2
Invitado	1. a) 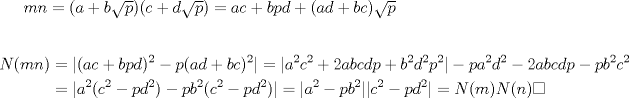$TEX: $mn=(a+b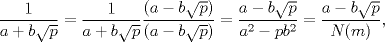\sqrt{p})(c+d\sqrt{p})=ac+bpd+(ad+bc)\sqrt{p}$<br /><br />\begin{align}<br />N(mn)&=\|(ac+bpd)^2-p(ad+bc)^2\|=\|a^2c^2+2abcdp+b^2d^2p^2\|-pa^2d^2-2abcdp-pb^2c^2\\<br />&=\|a^2(c^2-pd^2)-pb^2(c^2-pd^2)\|=\|a^2-pb^2\|\|c^2-pd^2\|=N(m)N(n)\square<br />\end{align}$ b) $TEX: $\dfrac{1}{a+b\sqrt{p}}=\dfrac{1}{a+b\sqrt{p}}\dfrac{(a-b\sqrt{p})}{(a-b\sqrt{p})}=\dfrac{a-b\sqrt{p}}{a^2-pb^2}=\dfrac{a-b\sqrt{p}}{N(m)},$$ luego si 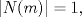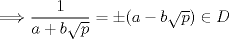$TEX: $\|N(m)\|=1,$$ $TEX: $\Longrightarrow \dfrac{1}{a+b\sqrt{p}}=\pm (a-b\sqrt{p})\in D$$ La implicación hacia la izquierda es debido a que si 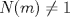$TEX: $N(m)\neq 1$$ los coeficientes serán raciones no naturales ya que $p$ es primo y entonces... Mañana termino la implicación izquierda, me dio sueño

DressedToKill Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 27 2009, 02:21 AM Publicado: #3
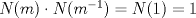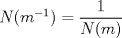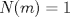Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.818 Registrado: 21-December 06 Miembro Nº: 3.434	La implicancia hacia la izquierda es la que hiciste ahí. Para la derecha, basta con notar que $TEX: $N(m) \cdot N(m^{-1}) = N(1) = 1$$ , de donde $TEX: $N(m^{-1}) = \dfrac{1}{N(m)}$$ . Pero $TEX: $N(a) \in \mathbb{Z}, \forall a \in \mathbb{Z}[\sqrt{p}]$$ , luego $TEX: $N(m)=1$$ . -------------------- http://www.youtube.com/watch?v=sp_WV91jx8E...feature=related

Abu-Khalil Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 5 2009, 08:33 PM Publicado: #4
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	2a $TEX: \noindent $R_1\not=\emptyset$ pues $1e=e\in R_1$. Sean $x_1e,x_2e\in R_1$. Entonces <br />\[x_1e+x_2e=\left(\underbrace{x_1+x_2}_{\in R}\right)e\in R_1 \qquad \land \qquad \underbrace{x_1e x_2}_{\in R}e\in R_1.\]<br />Luego, $R_1$ es un subanillo. $\square$<br />$ 2b $TEX: \noindent Considere $R_2=\left\{x(1-e):x\in R\right\}$. $R_2\not=\emptyset$ pues $1(1-e)=(1-e)\in R_2$. Sean $x_1(1-e),x_2(1-e)\in R_2,$ entonces<br />\[x_1(1-e)+x_2(1-e)=\left(\underbrace{x_1+x_2}_{\in R}\right)(1-e)\in R_2 \qquad \land \qquad \underbrace{x_1(1-e)x_2}_{\in R}(1-e)\in R_2.\]<br />Luego, $R_2$ es un subanillo.\\<br />\\<br />Sea $x\in R$. Como $x=1+xe-xe=xe+x(1-e)$, se tiene que $R=R_1+R_2$. Sea $y\in R_1\cap R_2$, entonces<br />\[y=x_1e=x_2(1-e)\Rightarrow x_1e=x_1e^2=x_2\left(1-e\right)e=x_20=0\Rightarrow y=0;\]<br />pues por hipótesis $e^2=e\Rightarrow e(1-e)=0$. $\therefore R_1\oplus R_2=R$. $\square$<br />$ -------------------- ~milopez $TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]$ $TEX: <br />\begin{equation}\begin{aligned}<br />dS_t&=\mu S_t dt+\sqrt{V_t}S_t dW^S_t\\<br />dV_t&=\kappa(\theta-V_t)dt+\sigma\sqrt{V_t} dW^V_t\\<br />\end{aligned}\end{equation}<br />$ $TEX: <br />$$\mathbb A^{\text U}_M(N)$$<br />$

Abu-Khalil Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 7 2009, 04:40 PM Publicado: #5
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	3a $TEX: \noindent Sea $g(x)=\sum_{i=0}^n\overline{a_i}x^i,$ entonces basta tomar $f(x)=\sum_{i=0}^na_ix^i$ y sigue que<br />\[\Phi\left(f(x)\right)=g(x).\]<br />$ 3b $TEX: \noindent Como $f(x)$ es un polinomio mónico, se tiene que<br />\[f(x)=a_0+a_1x+\ldots+a_{n-1}x^{n-1}+x^n;\]<br />con $a_i\in\mathbb{Z}$. Supongamos que $f(x)$ no es irreducible en $\mathbb{Z}[x]$, entonces existen<br />\[p(x)=b_0+b_1x+\ldots+b_mx^m \qquad , \qquad q(x)=c_0+c_1x+\ldots+c_rx^r;\]<br />tales que $m+r=n;b_j,c_k\in\mathbb{Z};m,r\geq 1$ y además,<br />$f(x)=p(x)q(x).$ Luego, como $b_mc_r=1\Rightarrow b_m=c_r=1=\overline{b_m}=\overline{c_r}$.\\<br />\\<br />Así, $\partial \overline{p(x)}=m$ y $\partial \overline{q(x)}=r$. Luego, dado que $p$ es primo, sigue que $\overline{f(x)}=\overline{p(x)}\overline{q(x)}$ con $\overline{p(x)},\overline{q(x)}$ no unidades pues son mónicos.\\<br />\\<br />Luego, $f(x)$ es irreducible en $\mathbb{Z}[x]$ y por lo tanto, en $\mathbb{Q}[x]$. $\square$$ 3c $TEX: \noindent Tomando $p=5$, se tiene que $g(x)=\Phi(f(x))=x^4+2.$\\<br />\\<br />Mostraremos que este polinomio es irreducible en $\mathbb{Z}_p$. Supongamos que no lo fuese, entonces $g(x)=p(x)q(x)$ con $p(x),q(x)$ no unidades. Entonces, \[\partial p(x)=1\land \partial q(x)=3\qquad \lor \qquad \partial p(x)=\partial q(x)=2.\]<br />Pero $x^4\not= 3\mod 5, \forall x=1,2,3,4$. Luego, no puede tener raíces y por lo tanto, se descarta la primera opción. La segunda opción, tampoco puede ser (se deja al esforzado lector cuadrar coeficientes). Por lo tanto, es irreducible. $\square$<br />$ -------------------- ~milopez $TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]$ $TEX: <br />\begin{equation}\begin{aligned}<br />dS_t&=\mu S_t dt+\sqrt{V_t}S_t dW^S_t\\<br />dV_t&=\kappa(\theta-V_t)dt+\sigma\sqrt{V_t} dW^V_t\\<br />\end{aligned}\end{equation}<br />$ $TEX: <br />$$\mathbb A^{\text U}_M(N)$$<br />$

coquitao Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 7 2009, 05:07 PM Publicado: #6
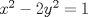Dios Matemático Supremo Grupo: Super Moderador Mensajes: 2.065 Registrado: 25-May 08 Desde: Pelotillehue Miembro Nº: 24.463	1.c. La ecuación de Pell $TEX: $x^{2}-2y^{2}=1$$ tiene infinitas soluciones en enteros positivos. Cada solución (x,y) da lugar a un elemento invertible de $TEX: $\mathbb{Z}[\sqrt{2}]$.$ Fin. -------------------- "Please forget everything you have learned in school; for you haven't learned it... Please keep in mind at all times the corresponding portions of your school curriculum; for you haven't actually forgotten them." -- E. Landau

DressedToKill Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 7 2009, 05:39 PM Publicado: #7
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.818 Registrado: 21-December 06 Miembro Nº: 3.434	CITA(coquitao @ Nov 7 2009, 06:07 PM) 1.c. La ecuación de Pell 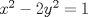$TEX: $x^{2}-2y^{2}=1$$ tiene infinitas soluciones en enteros positivos. Cada solución (x,y) da lugar a un elemento invertible de $TEX: $\mathbb{Z}[\sqrt{2}]$.$ Fin. Una solución sin ecuaciones de Pell es lo que se pedía en la prueba... Pell no es un tema de ese curso. -------------------- http://www.youtube.com/watch?v=sp_WV91jx8E...feature=related

« Posterior · Álgebra Abstracta · Anterior »

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 29th October 2025 - 04:55 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.