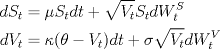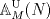Examen Álgebra Abstracta - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa Enseñanza Universitaria > Comunidades Universitarias > Universidad Católica > Álgebra Abstracta

Reply to this topic

Start new topic

Examen Álgebra Abstracta, 1-2009

DressedToKill Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 27 2009, 12:51 AM Publicado: #1
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.818 Registrado: 21-December 06 Miembro Nº: 3.434	Examen del primer semestre 2009, prof. Ángel Carocca. $TEX: \noindent<br />\begin{center}\bf{EXAMEN\\<br />MAT 2205 - ALGEBRA ABSTRACTA I} \end{center}<br /><br />\begin{enumerate}<br /><br />\item Considere $K$ un cuerpo con $\|K : \mathbb{Q}\| = m$ y $f(x) \in \mathbb{Q}[x]$ un polinomio irreducible sobre $\mathbb{Q}$ con $\delta(f(x)) = n$. \\<br />Pruebe que si $(n,m) = 1$, entonces $f(x)$ es irreducible sobre $K$.<br /><br />\item Sea $G$ un grupo con $\|G\| = 12$ y NO isomorfo a $A_4$. \\<br />Decida si las siguientes afirmaciones son verdaderas o falsas. Justifique cada una de sus respuestas.<br /><br />\begin{enumerate}<br /><br />\item $\|Syl_3(G)\| = 1$.<br /><br />\item Existe $g \in G$ con $\|g\| = 6$.<br /><br />\item $Z(G) \not = 1$<br /><br /><br />\end{enumerate}<br /><br /><br />\item Un elemento no invertible $d$ de un anillo $R$ se dice irreducible si vale: "Si $d = ab$ con $a,b \in R$ entonces $a$ es invertible en $R$ o $b$ es invertible en $R$". \\<br />Sea $R = \mathbb{Z}[i]$. Pruebe las siguientes afirmaciones:<br /><br />\begin{enumerate}<br /><br />\item $u = 1+ 2i$ es irreducible.<br /><br />\item $v = 4 + 3i$ no es irreducible.<br /><br />\item $R \backslash <v>$ tiene divisores de cero.<br /><br />\item $\overline{3+i}$ no es invertible en $R \backslash <u>$.<br /><br />\end{enumerate}<br /><br />\item Determine todos los grupos finitos con exactamente tres clases de conjugación.<br /><br />\item Sean $f(x) = x^4+1 \in \mathbb{Q}[x]$ y $L = Gal(f(x),\mathbb{Q})$. \\<br />Determine <br /><br />\begin{enumerate}<br /><br />\item $\|L : \mathbb{Q}\|$.<br /><br />\item Una base para $L$ sobre $\mathbb{Q}$.<br /><br />\item $Aut(L)$.<br /><br />\end{enumerate}<br /><br />\end{enumerate}<br /><br />$ $TEX: \begin{enumerate}<br /><br />\item[6.] Sean $p$ un número primo y<br />$$A = \left\{ \dfrac{m}{n} / m,n \in \mathbb{Z}, n \not = 0, (p,n) = 1 \right\}$$<br /><br />Pruebe las siguientes afirmaciones<br /><br />\begin{enumerate}<br /><br />\item $ A \le_a \mathbb{Q}$.<br /><br />\item $I = \left\{ \dfrac{m}{n} \in A / p \| m \right\}$ es un ideal de $A$.<br /><br />\end{enumerate}<br /><br /><br />\end{enumerate}<br /><br />$ Comentarios: En el examen había que elegir 4 de los 6 problemas. En las preguntas 1 y 5, 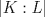$TEX: $\|K : L\|$$ es la dimensión de K como L-espacio vectorial. En la 3, 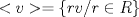$TEX: $<v> = \{r v / r \in R \}$$ . Yo encontre dificil el examen incluso con la opción de elegir preguntas, la 6 era regalada si. -------------------- http://www.youtube.com/watch?v=sp_WV91jx8E...feature=related

DressedToKill Ver Perfil del Miembro Ver los mensajes de este miembro	Sep 13 2009, 09:10 PM Publicado: #2
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.818 Registrado: 21-December 06 Miembro Nº: 3.434	Dejo la respuesta de la 1. $TEX: \noindent<br />Sea $\alpha$ raíz de $f$, entonces $\alpha \not \in K$. En efecto, si $\alpha \in K$ entonces $\mathbb{Q}(\alpha) \le_C K$, que sería una contradicción pues se tendría $[\mathbb{Q}(\alpha):\mathbb{Q}] \| [K:\mathbb{Q}]$, es decir, $n \| m$. \\<br />Luego, $[K(\alpha):K] > 1$ y se tienen las siguientes igualdades \\<br />(1) \quad $[K(\alpha):\mathbb{Q}] = [K(\alpha):K][K:\mathbb{Q}]$ \\<br />(2) \quad $[K(\alpha):\mathbb{Q}] = [K(\alpha):\mathbb{Q}(\alpha)][\mathbb{Q}(\alpha):\mathbb{Q}]$ \\<br />Así, se tiene $m \| [K(\alpha):\mathbb{Q}]$, $n \| [K(\alpha):\mathbb{Q}]$ y entonces $[K(\alpha):\mathbb{Q}] \ge mn$. \\<br />Además, como $f \in K[x]$, $f(\alpha) = 0$ y $\delta(f) = n$ entonces se tiene que\\ $[K(\alpha):K] \le n$, y luego, de (1) se concluye que $[K(\alpha):\mathbb{Q}] \le mn$, es decir,\\ $[K(\alpha):\mathbb{Q}] = mn$. \\<br />Entonces, $[K(\alpha):K] = n$ y por lo tanto $f$ es irreducible en $K$, ya que en caso contrario, existiría $g \in K[x]$ tal que $g(\alpha) = 0$ y $\delta(g) < n$, con lo que se tendría $[K(\alpha):K] < n$, que es una contradicción.<br />$ -------------------- http://www.youtube.com/watch?v=sp_WV91jx8E...feature=related

Abu-Khalil Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 11 2009, 08:09 PM Publicado: #3
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	P2a) $TEX: \noindent En general, para todo grupo $G$ de orden $12$ se tiene que $r_3\in\left\{1,4\right\}$. Mostraremos que si $r_3=4\Rightarrow G\cong A_4$.\\<br />\\<br />Sea Syl$_3(G)=\left\{H_i\right\}$, con $i=1,2,3,4$. Consideremos la acción de grupo de $G$, dada por<br />\[\begin{tabular}{c c c c}<br />$\tau_g:$&Syl$_3(G)$&$\to$&Syl$_3(G)$\\<br />&$H_i$&$\to$&$gH_ig^{-1}$<br />\end{tabular}.<br />\]<br />Esta acción induce un homomorfismo<br />\[\begin{tabular}{c c c c}<br />$\varphi:$&$G$&$\to$&Im$\varphi\leq S_4$\\<br />&$g$&$\to$&$\tau_g$<br />\end{tabular}.<br />\]<br />Notemos que <br />\[\ker\varphi=\left\{g\in G:\tau_g = I\right\}=\left\{g\in G:gH_ig^{-1} = H_i,\forall i\right\}=\left\{e\right\};\]<br />pues las órbitas de conjugación en Syl$_p(G)$ son todo el conjunto. Luego, $G\cong \operatorname{Im}\varphi\Rightarrow \|\operatorname{Im}\varphi\|=12\Rightarrow \operatorname{Im}\varphi=A_4$, pues es el único subgrupo de orden 12 de $S_4$. Por lo tanto, la afirmación es verdadera.<br />$ -------------------- ~milopez $TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]$ $TEX: <br />\begin{equation}\begin{aligned}<br />dS_t&=\mu S_t dt+\sqrt{V_t}S_t dW^S_t\\<br />dV_t&=\kappa(\theta-V_t)dt+\sigma\sqrt{V_t} dW^V_t\\<br />\end{aligned}\end{equation}<br />$ $TEX: <br />$$\mathbb A^{\text U}_M(N)$$<br />$

Abu-Khalil Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 26 2009, 07:58 PM Publicado: #4
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	P3 $TEX: \begin{enumerate}<br />\item[$i$)]Consideramos $N(1+2i)=5$. Como $5$ es primo, entonces $1+2i$ es irreducible en $\mathbb{Z}[i]$.<br />\item[$ii)$]Notamos que $4+3i=(2-i)(1+2i)$ y por lo tanto, no es irreducible.<br />\item[$iii)$]Como $v$ no es irreducible $\Rightarrow v$ es primo $\Rightarrow <v>$ no es un ideal primo $\Rightarrow \mathbb{Z}[i]/<v>$ no es dominio. Pero $\mathbb{Z}[i]$ es conmutativo y unitario y por lo tanto, $\mathbb{Z}[i]/<v>$ debe tener divisores del cero.<br />\end{enumerate}$ -------------------- ~milopez $TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]$ $TEX: <br />\begin{equation}\begin{aligned}<br />dS_t&=\mu S_t dt+\sqrt{V_t}S_t dW^S_t\\<br />dV_t&=\kappa(\theta-V_t)dt+\sigma\sqrt{V_t} dW^V_t\\<br />\end{aligned}\end{equation}<br />$ $TEX: <br />$$\mathbb A^{\text U}_M(N)$$<br />$

Abu-Khalil Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 26 2009, 07:58 PM Publicado: #5
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	P6b $TEX: \noindent Es fácil ver que $I$ es cerrado bajo suma y multiplicación. Supongamos que $\exists x\in R-I$ tal que $ix\not\in I$ para algún $i\in I$. Entonces, si $ix=\frac{i_1x_1}{i_2x_2}=\frac{a}{b}\Rightarrow p$ no divide a $a$ y entonces, como $p$ es primo, $p\|x_2$. $\square$$ -------------------- ~milopez $TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]$ $TEX: <br />\begin{equation}\begin{aligned}<br />dS_t&=\mu S_t dt+\sqrt{V_t}S_t dW^S_t\\<br />dV_t&=\kappa(\theta-V_t)dt+\sigma\sqrt{V_t} dW^V_t\\<br />\end{aligned}\end{equation}<br />$ $TEX: <br />$$\mathbb A^{\text U}_M(N)$$<br />$

Sergy Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 8 2012, 02:49 PM Publicado: #6
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 145 Registrado: 21-June 07 Desde: Quilicura Miembro Nº: 6.942 Nacionalidad: Universidad: Sexo:	$TEX: 2.\\<br />b) \ Como $2\| \|G\|$ y $3\|\|G\|$, por Cauchy existen $h,k\in G$ con $\|h\|=2$ y $\|k\|=3$ luego tomando $g=hk$ tenemos $\|g\|=6$.\\<br /><br />c) Como $G$ tiene un $syl_3(G)$, sea $P$, y si hubiese solo un $syl_2(G)$,sea $Q$, además de que $\|P\cap Q\|=1$ tenemos:\\<br /><br />$G \cong P \times Q$.\\<br /><br />De $P\cong \mathbb{Z}_3$ y de, $Q\cong \mathbb{Z}_4$ ó $Q\cong \mathbb{Z}_2\times \mathbb{Z}_2$ conseguimos:\\<br /><br />$G\cong \mathbb{Z}_6\times \mathbb{Z}_2$ ó $G\cong \mathbb{Z}_3\times \mathbb{Z}_4$, ambos casos abelianos luego $Z(G)=G$.\\<br /><br />El caso cuando hay 3 $syl_2(G)$ aún lo estoy pensando pero parece que voy a tener que aprender producto semidirecto primero.<br />$ Mensaje modificado por Sergy el Jan 8 2012, 09:51 PM

Sergy Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 8 2012, 11:03 PM Publicado: #7
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 145 Registrado: 21-June 07 Desde: Quilicura Miembro Nº: 6.942 Nacionalidad: Universidad: Sexo:	$TEX: 4.\\<br /><br />Consideremos la acción por conjugación de $G$ sobre si mismo $G$. Esta induce un homomorfismo $\psi:G \rightarrow S_3$ cuyo kernel es el centro de $G$; $Z(G)$, entonces:\\<br /><br />$G/Z(G)\cong$ a un subgrupo de $S_3$, luego $\|G/Z(G)\|=1,2,3$ ó 6.\\<br /><br />Si $\|G/Z(G)\|=1$ entonces $G$ es abeliano con 3 clases de conjugación, luego $G\cong \mathbb{Z}_3$.\\<br /><br />Si $\|G/Z(G)\|=p$ con $p$ primo entonces $G$ es abeliano (esto es un ejercicio) y volvemos al caso anterior.\\<br /><br />Si $\|G/Z(G)\|=6$ entonces $G\cong S_3$.<br /><br />$

Sergy Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 8 2012, 11:51 PM Publicado: #8
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 145 Registrado: 21-June 07 Desde: Quilicura Miembro Nº: 6.942 Nacionalidad: Universidad: Sexo:	$TEX: 5.\\<br /><br />Como $f(x)=\phi_8=x^4+1$ vemos que $L=\mathbb{Q}(\zeta_8)$, con lo que tenemos:\\<br /><br />a) \ $[L:\mathbb{Q}]=4$\\<br /><br />b) \ Una $\mathbb{Q}$ base para $L$ sería el conjunto $\{1,\zeta_8^3,\zeta_8^5,\zeta_8^7\}$\\<br /><br />c) \ $Gal(L)\cong \left( \mathbb{Z}/ 8\mathbb{Z}\right)^{\times}$\\<br /><br />Nota: $\phi_8$ es el polinomio ciclotómico de las raíces octavas priimitivas de la unidad.<br /><br />$ Mensaje modificado por Sergy el Jan 8 2012, 11:54 PM

Sergy Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 8 2012, 11:56 PM Publicado: #9
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 145 Registrado: 21-June 07 Desde: Quilicura Miembro Nº: 6.942 Nacionalidad: Universidad: Sexo:	$TEX: <br />¿qué es $\leq_a$?<br />$

lokko62 Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 9 2012, 12:12 AM Publicado: #10
Maestro Matemático Grupo: Usuario FMAT Mensajes: 73 Registrado: 9-May 08 Miembro Nº: 22.618 Nacionalidad: Sexo:	CITA(Sergy @ Jan 9 2012, 12:56 AM) $TEX: <br />¿qué es $\leq_a$?<br />$ Subanillo -------------------- http://facebook/niumbrillo https://twitter.com/#!/niumbrillo CITA(Pasten) Estimados, He bajado del olimpo para hacerme presente, quebrarme y molestar. Procedo: Usuario: Oh ilustre Pasten, que nos honras con tu presencia, llegara el dia en que podamos ver la vida desde el pedestal de bacanidad en el que tu, oh ser magnifico, contemplas nuestras burdas conversaciones? Pasten: No. Saludos CITA(Sansanito) Es re fácil entrar a princeton... no tiene ni rejas....

« Posterior · Álgebra Abstracta · Anterior »

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 29th October 2025 - 04:55 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.