I2 Álgebra Abstracta - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa Enseñanza Universitaria > Comunidades Universitarias > Universidad Católica > Álgebra Abstracta

Reply to this topic

Start new topic

I2 Álgebra Abstracta, 1-2009

DressedToKill Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 27 2009, 01:29 AM Publicado: #1
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.818 Registrado: 21-December 06 Miembro Nº: 3.434	$TEX: \noindent<br /><br />\begin{center} \bf{INTERROGACION II \\ MAT2205 - ALGEBRA ABSTRACTA I} \end{center}<br /><br />\begin{enumerate}<br /><br />\item Sea $G$ un grupo tal que $\|G\| = pqr$ con $p,q$ y $r$ números primos. \\<br />Pruebe que $G$ tiene un subgrupo de Sylow normal, para algún primo divisor de $\|G\|$.<br /><br />\item Sea $G$ un grupo finito. Un subgrupo $M < G$ se dice maximal (escribiremos $M < \cdot G$) si <br />$$ M \le X < G \Rightarrow M = X $$<br />Sea $\Phi(G) = \displaystyle\bigcap_{M < \cdot G} M$. Pruebe las siguientes afirmaciones<br /><br />\begin{enumerate}<br /><br />\item Sea $H \le G$. Si $G = H \Phi(G)$, entonces $H = G$.<br /><br />\item $\|Syl_p (G)\| = 1$ para todo primo $p$ divisor de $\|\Phi(G)\|$.<br /><br />\item Si $G/\Phi(G)$ es soluble, entonces $G$ es soluble.<br /><br />\end{enumerate}<br /><br /><br />\item Describa la estructura del grupo $G = SL(2,3)$.<br /><br /><br /><br /><br /><br /><br />\end{enumerate}<br /><br />$ La prueba de enunciado más corto, pero fue la más dificil... El problema 3 era un cacho y el 1 también era quitatiempo. El 2 no era largo pero era bastante respetable. En la pregunta 3, SL(2,3) corresponde a las matrices de 2x2 con coeficientes en Z_3 con determinante 1. Describir la estructura es basicamente encontrar todos los subgrupos de Sylow, decir el orden del grupo, encontrar su centro y los normalizadores de cada subgrupo de Sylow. -------------------- http://www.youtube.com/watch?v=sp_WV91jx8E...feature=related

Abu-Khalil Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 9 2009, 11:17 PM Publicado: #2
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \noindent Por Sylow, tenemos que<br />\[r_p=\begin{cases}<br />1\\<br />q\\<br />r\\<br />qr<br />\end{cases} \qquad ; \qquad <br />r_q=\begin{cases}<br />1\\<br />p\\<br />r\\<br />pr<br />\end{cases} \qquad ; \qquad <br />r_r=\begin{cases}<br />1\\<br />p\\<br />q\\<br />pq<br />\end{cases}.<br />\]<br />Supongamos que todos son distintos de 1. Distingamos dos casos generales<br />\begin{enumerate}<br />\item Supongamos que $r_p=q\Rightarrow q\equiv 1\mod p\Rightarrow q>p$. Luego, $r_q=r,pr$.<br />\begin{enumerate}<br />\item Si $r_q=r\Rightarrow r\equiv 1\mod q\Rightarrow r>q>p\Rightarrow r_r=pq$. Contando el número de elementos:<br />\begin{equation}\begin{aligned}<br />\|G\|&\geq 1+(p-1)q+(q-1)r+(r-1)pq=1+pq-q+rq-r+pqr-pq\\<br />&\geq 1+pqr+rq-(q+r)\geq 1+pqr.<br />\end{aligned}\end{equation}<br />\item Si $r_q=pr\Rightarrow r_r=p,q,pq$.<br />\begin{enumerate}<br />\item Si $r_r=p$, contando el número de elementos:<br />\begin{equation}\begin{aligned}<br />\|G\|&\geq 1+(p-1)q+(q-1)pr+(r-1)p=1+pq-q+pqr-pr+pr-p\\<br />&\geq 1+pqr+pq-(q+p)\geq 1+pqr.<br />\end{aligned}\end{equation}<br />\item Si $r_r=q$, contando el número de elementos:<br />\begin{equation}\begin{aligned}<br />\|G\|&\geq 1+(p-1)q+(q-1)pr+(r-1)q=1+pq-q+pqr-pr+qr-q\\<br />&\geq 1+pqr+(q-p)r+(p-2)q\geq 1+pqr.<br />\end{aligned}\end{equation}<br />\item Si $r_r=pq$, tenemos más elementos que en los dos casos anteriores, así que tampoco es factible.<br />\end{enumerate}<br />\end{enumerate}<br />\item Si $r_p=rq\Rightarrow r_q=p,r,pr$<br />\begin{enumerate}<br />\item Si $r_q=p\Rightarrow p\equiv 1\mod p\Rightarrow p>q$ y el resto sigue análogo. $\square$<br />\end{enumerate}<br />\end{enumerate}<br />$ Se usó que 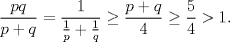$TEX: $\displaystyle\frac{pq}{p+q}=\frac{1}{\frac{1}{p}+\frac{1}{q}}\geq \frac{p+q}{4}\geq \frac{5}{4}>1.$$ PD: Dado mi nulo conocimiento de Teo de números, probablemente hayan pasos que sean más cortos -------------------- ~milopez $TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]$ $TEX: <br />\begin{equation}\begin{aligned}<br />dS_t&=\mu S_t dt+\sqrt{V_t}S_t dW^S_t\\<br />dV_t&=\kappa(\theta-V_t)dt+\sigma\sqrt{V_t} dW^V_t\\<br />\end{aligned}\end{equation}<br />$ $TEX: <br />$$\mathbb A^{\text U}_M(N)$$<br />$

« Posterior · Álgebra Abstracta · Anterior »

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 29th October 2025 - 04:53 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.