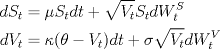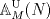|
|
|
|
|
|
|
  |
 Jul 27 2009, 02:09 AM Jul 27 2009, 02:09 AM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.818 Registrado: 21-December 06 Miembro Nº: 3.434 |
Prof. Marta García-Huidobro.
![TEX: \noindent<br /><br />\begin{center} \bf{Análisis Real, Interrogación N°2} \\ Lunes 6 de Octubre, 2008 \end{center}<br /><br />\begin{enumerate}<br /><br />\item Sea $X = \{f: [0,1] \to \mathbb{R} : f$ es diferenciable en $[0,1] \}$, con la métrica $\rho:X \times X \to \mathbb{R}$ definida por $\rho(f,g) = \displaystyle\sup_{x \in [0,1]} |f(x) - g(x)|$. Pruebe que $(X, \rho)$ no es completo.<br /><br />\item Sea $(X, d)$ espacio métrico. <br /><br />\begin{enumerate}<br /><br />\item Sean $F,K$ subconjuntos de $X$. Demuestre que si $F$ es cerrado y $K$ es compacto, entonces $F \cap K$ es compacto.<br /><br />\item Sea $\mathcal{F}$ una colección infinita de subconjuntos compactos de $X$. Demuestre que $\displaystyle\bigcap_{F \in \mathcal{F}} F$ es un conjunto compacto.<br /><br />\item Demuestre que la unión de un número finto de subconjuntos compactos de $X$ es un conjunto compacto.<br /><br />\end{enumerate}<br /><br />\item Demuestre que si un subconjunto $E$ de un espacio métrico es conexo, entonces $\overline{E}$ también es conexo. Si $\overline{E}$ es conexo, ¿es $E$ necesariamente conexo?.<br /><br />\item Denotemos por $B([0,1])$ el conjunto de todas las funciones acotadas de $[0,1]$ en $\mathbb{R}$.\\ Para $f, g \in B([0,1])$, definamos $d(f,g) = \sup\{|f(x)-g(x)|/x \in [0,1] \}$. Sea $f_0: [0,1] \to \mathbb{R}$ la función nula, es decir, $f_0(x) = 0$ para todo $x \in [0,1]$. Demuestre que el conjunto <br />$$\overline{\{f \in B([0,1]) / d(f,f_0) < 1 \}}$$<br />es acotado y cerrado pero NO es compacto.<br /><br />\end{enumerate}<br /><br />](./tex/e1bda532d5bc1769b29b99ad4d292091.png)
-------------------- |
|
|
|
 Jul 27 2009, 11:32 AM Jul 27 2009, 11:32 AM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Super Moderador Mensajes: 1.912 Registrado: 10-January 08 Desde: Un Sobolev Miembro Nº: 14.530 Nacionalidad:  Sexo:  |
-------------------- |
|
|
|
 Sep 10 2009, 10:58 PM Sep 10 2009, 10:58 PM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
P3
![TEX: \noindent Sean $G_1,G_2$ dos abiertos no vacíos tales que <br />\begin{enumerate}<br />\item $G_1\cap \overline{E}\not=\emptyset$.<br />\item $G_1\cap G_2\cap\overline{E}=\emptyset$.<br />\item $\overline{E}\subseteq G_1\cup G_2$.<br />\end{enumerate}<br />Como $E\subseteq \overline{E}$, entonces <br />\begin{enumerate}<br />\item $G_1\cap G_2\cap E=\emptyset$.<br />\item $E\subseteq G_1\cup G_2$.<br />\end{enumerate}<br />Si $G_1\cap E=\emptyset$, entonces existe $p\in E'$ tal que $p\in G_1$, pero como $G_1$ es abierto, $\exists r>0$ tal que $B(p,r)\subset G_1$ y sigue que $G_1\cap E\not=\emptyset$. Luego, como $E$ es conexo $G_2\cap E=\emptyset$ y por un razonamiento análogo al anterior, $G_2$ no puede contener puntos límites de $E$. Así, $G_2\cap \overline{E}=\emptyset.$<br />\begin{flushright}<br />$\square$<br />\end{flushright}<br />Sea $E=(0,1)\cup(1,2)\subset \mathbb{R}$ usual. Como un conjunto es conexo en $\mathbb{R}$ ssi es un intervalo, entonces $\overline{E}=[0,2]$ es conexo pero no $E$.<br />](./tex/5df8ffe373f35083d73fb84c1627b5be.png)
-------------------- |
|
|
|
 Sep 19 2009, 10:44 PM Sep 19 2009, 10:44 PM
Publicado:
#4
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
P2b)
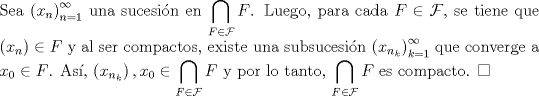 P2c) 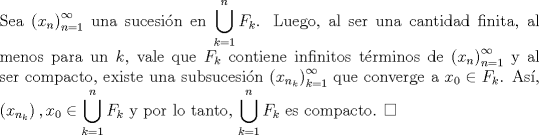
-------------------- |
|
|
|
 Sep 20 2009, 12:38 PM Sep 20 2009, 12:38 PM
Publicado:
#5
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad:  Colegio/Liceo:  Sexo:  |
![TEX: $ $\\<br />Agradecimientos a quienes desenterraron este tema (yo nunca lo vi)\\<br />$ $\\<br />Soluci\'on a la primera parte del problema 4.\\<br />$ $\\<br />Hasta donde se todas las clausuras son cerradas por un teorema muy com\'un.\\<br />Para mostrar acotamiento sea $f\in\mathcal{\mathbf{B}}_{[0,1]}$, entonces $|f|\leq|f-f_{0}|+|f_{0}|\leq1+0=1$.\\<br />As\'i que $\|\mathcal{\mathbf{B}}_{[0,1]}\|=\displaystyle\sup_{f\in\mathcal{\mathbf{B}}_{[0,1]}}\|f\|\leq1$.\\<br />](./tex/67b36aa40ab61946313b71100b290928.png)
Mensaje modificado por Kaissa el Sep 20 2009, 12:40 PM -------------------- |
|
|
|
 Oct 3 2009, 08:34 PM Oct 3 2009, 08:34 PM
Publicado:
#6
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
P4
![TEX: \noindent Consideremos <br />\[f_n(x)=\begin{cases}\begin{tabular}{c c c}<br />$\dfrac{\sqrt{\pi}}{17},$&si&$x=\dfrac{1}{n}$;\\<br />\\<br />$0$,&si&$x\not=\dfrac{1}{n}$.<br />\end{tabular}\end{cases}\]<br />Como $\frac{\sqrt{\pi}}{17}<1\Rightarrow \left(f_n\right)\in B[0,1]$. Notemos que $d(f_n,f_m)=\frac{\sqrt{\pi}}{17},\forall n,m$ distintos.\\<br />\\<br />Luego, cualquier subsucesión de $\left(f_n\right)$ no es de Cauchy y por ende, no puede ser convergente. Así, el conjunto no es compacto. $\square$<br />](./tex/84c8d1b6ec87fb810e4ac8605db9e682.png)
-------------------- |
|
|
|
 Jan 29 2012, 12:29 AM Jan 29 2012, 12:29 AM
Publicado:
#7
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 465 Registrado: 15-July 11 Miembro Nº: 91.905 Nacionalidad:  Universidad:  Sexo:  |
P3.
Suponga que 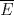 no es conexo. Entonces existe no es conexo. Entonces existe 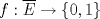 continua y sobre. Como continua y sobre. Como 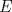 es conexo, entonces es conexo, entonces 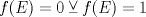 (pues si (pues si 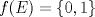 se cumpliría que se cumpliría que 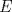 no es conexo). Asuma w.l.o.g que no es conexo). Asuma w.l.o.g que 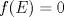 . Sea . Sea 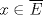 y y 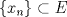 una sucesión tal que una sucesión tal que  cuando cuando 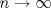 . Como . Como 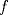 es continua, se tiene que es continua, se tiene que 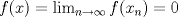 . Esto significa que . Esto significa que 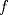 no es sobre. Contradicción. Por lo tanto no es sobre. Contradicción. Por lo tanto 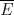 es conexo. es conexo.  Para el contraejemplo, basta ver el post de Abu-Khalil. Mensaje modificado por Cenizas con Mostaza el Jan 29 2012, 10:03 AM -------------------- He-llo? Could you say that again? More slowly? In a language I understand? Depending on what you said, I might kick your ass! |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 29th October 2025 - 08:20 AM |












![TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]](./tex/e0e88dba678ca3ead120b088f41191b2.png)