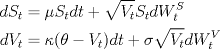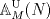|
|
|
|
|
|
|
  |
 Jul 27 2009, 11:51 PM Jul 27 2009, 11:51 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.818 Registrado: 21-December 06 Miembro Nº: 3.434 |
![TEX: \noindent<br /><br />\begin{center} \bf{Interrogación N. 3, Análisis Real} \\ Lunes 10 de Noviembre, 2008 \end{center}<br /><br />\begin{enumerate}<br /><br />\item<br /><br />\begin{enumerate}<br /><br />\item Sea $(X,d)$ un espacio métrico compacto, y sea $\{x_n\}$ una sucesión en $X$ tal que toda subsucesión de ella que converge, converge a $x_0 \in X$. Demuestre que $\displaystyle\lim_{n \to \infty} x_n = x_0$.<br /><br />\item Dé un ejemplo para mostrar que la hipótesis "compacto" es necesaria.<br /><br />\end{enumerate}<br /><br />\item<br /><br />\begin{enumerate}<br /><br />\item Sea $f_n:[0,1] \to \mathbb{R}$ definida por<br />$$f_n(x) = \dfrac{nx}{1+n^2x^p}, \qquad p >0 $$<br />Determine los valores de $p$ para los cuales la sucesión $f_n$ converge uniformemente a su límite $f$.<br /><br />\item Considere la serie de funciones<br />$$\displaystyle\sum_{n=1}^{\infty} e^{-nx} \sin(nx)$$<br />Demuestre que esta serie converge puntualmente en $[0,\infty)$, uniformemente en $[\rho, \infty)$ para todo $\rho > 0$, pero no converge uniformemente en $[0,\infty)$.<br /><br />\end{enumerate}<br /><br />\item Un punto $x_0$ en un espacio métrico $(X,\rho)$ se dice aislado si existe una bola abierta $B_{\delta}(x_0)$ tal que $B_{\delta}(x_0) \cap X = \{ x_0 \}$. Pruebe que un espacio métrico completo que no tiene puntos aislados no puede ser numerable.<br /><br />\end{enumerate}<br /><br />](./tex/e9c4d75d53ad87a931504ceba0f95e35.png) ![TEX: \noindent<br /><br />\begin{enumerate}<br />\item[4.] Sea $(X,d)$ espacio métrico y sea $E \subset X$ un subconjunto con la siguiente propiedad: \\<br />Dado $\epsilon > 0$, existen puntos $x_1, x_2, \cdots, x_k$ de modo que $E \subset \displaystyle\bigcup_{i=1}^k B_{\epsilon}(x_i)$. (Los conjuntos con esta propiedad se llaman conjuntos totalmente acotados). <br /><br />\begin{enumerate}<br /><br />\item Muestre que un conjunto con la propiedad descrita arriba es acotado y de un ejemplo para mostrar que la afirmación recíproca no es necesariamente cierta.<br /><br />\item Demuestre que dada una sucesión $\{x_n\}$ en $E$, existen sucesiones $\{x_{1,n}\}, \{x_{2,n}\}, \{x_{3,n}\}, \cdots$ de manera que $\{x_{1,n}\} = \{x_n\}$, y para $k\ge2$<br /><br />\begin{enumerate}<br /><br />\item $\{x_{k,n}\}$ es una subsucesión de $\{x_{k-1,n}\}$, y <br /><br />\item $\{x_{k,n}\}$ está contenida en una bola de radio $1/k$.<br /><br />\end{enumerate}<br /><br /><br />Pruebe que $\{x_{n,n}\}$ es una subsucesión de Cauchy de $\{x_{n,n}\}$. Deduzca que en cualquier espacio métrico, un conjunto es compacto si y sólo si es totalmente acotado y completo.<br /><br /><br />\end{enumerate}<br />\end{enumerate}<br /><br />](./tex/f1a9f8513e86d1d602d1d345fbff5719.png)
-------------------- |
|
|
|
 Sep 26 2009, 01:12 PM Sep 26 2009, 01:12 PM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
-------------------- |
|
|
|
 Dec 7 2009, 09:31 PM Dec 7 2009, 09:31 PM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
P2a
![TEX: \noindent Es fácil ver que $f$ es la función nula. Luego, si $0<p\leq 1$<br />\[\sup_{x\in[0,1]}\left|\frac{nx}{1+n^2x^p}\right|\leq \frac{nx}{n^2x^p}=\frac{x^{1-p}}{n}\leq \frac{1}{n}\to 0.\]<br />Si $p>1$, notemos que<br />\[f_n'(x)=\frac{n\left(1+n^2x^p\right)-pn^3x^p}{\left((1+n^2x^p\right)^2}=0\iff n+n^3(1-p)x^p=0\iff x=\frac{1}{\sqrt[p]{n^2(p-1)}}.\]<br />Así,<br />\[\max_{x\in[0,1]}f\left(x\right)=\frac{\frac{n}{\sqrt[p]{n^2(p-1)}}}{1+\frac{1}{p-1}}=\frac{p-1}{p\sqrt[p]{p-1}}n^{1-\frac{2}{p}}.\]<br />$\therefore$ la convergencia es uniforme sólo si $1-\frac{2}{p}<0\iff p<2$. Finalmente, $f_n\to f$ uniformemente para $0<p<2$.<br />](./tex/29ef6305ea08cda93489274ad424e01d.png) P2b ![TEX: \noindent Sea $p>0$. Si $x\in[\rho,\infty)$, se tiene que<br />\[\left|e^{-nx}\sin nx\right|\leq e^{-nx}\leq e^{-n\rho}=M_n;\]<br />y por el criterio de Weiertrass, la serie converge uniformemente. Sin embargo, para cualquier $n\in\mathbb{N}$, se tiene que $\frac{1}{n}\in[0,\infty)$ y por lo tanto, <br />\[\sup_{x\in[0,1]}\left|e^{-nx}\sin nx\right|\geq e^{-1}\sin 1.\]<br />](./tex/4a4bd929fd99081ce8bf84795c03019c.png)
-------------------- |
|
|
|
 Dec 18 2010, 10:38 PM Dec 18 2010, 10:38 PM
Publicado:
#4
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 448 Registrado: 27-January 08 Miembro Nº: 15.045 Nacionalidad:  Sexo:  |
Pregunta 3
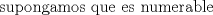 Por lo que 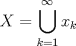 donde cada 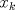 , es un punto de X , es un punto de Xes claro que como X no tiene puntos aislados cada 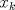 , es denso en ninguna parte por lo que X es de primera categoría, pero por el teorema de baire, y al ser X un espacio com´pleto X es de segunda categoría (es un abierto), se sigue la contradicción , es denso en ninguna parte por lo que X es de primera categoría, pero por el teorema de baire, y al ser X un espacio com´pleto X es de segunda categoría (es un abierto), se sigue la contradicción
Mensaje modificado por febomon el Dec 19 2010, 10:33 PM |
|
|
|
 Jul 4 2011, 12:13 AM Jul 4 2011, 12:13 AM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.767 Registrado: 21-January 08 Desde: Santiago - Ancud Miembro Nº: 14.865 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Demostraremos la 1a utilizando la siguiente caracterización de convergencia de sucesiones
http://www.fmat.cl/index.php?showtopic=706...mp;#entry538449 
-------------------- Estudia para superarte a ti mismo, no al resto. |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 29th October 2025 - 08:20 AM |










![TEX: \noindent Consideremos $X=\mathbb{N},$ equipado con la métrica usual restriginda de $\mathbb{R}$. Este espacio no es compacto pues no es acotado. Consideremos la sucesión <br />\[x_n=\begin{cases}<br />n,\text{ si }n\text{ es impar}\\<br />2,\text{ si }n\text{ es par}<br />\end{cases}.\]<br />Es claro que toda subsucesión que converge, lo hace a 2 pero $x_n\not \to 2$.<br />](./tex/ab39097fb3a61c2428b6ceee393fca87.png)
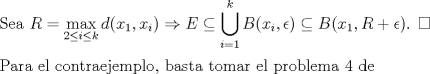

![TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]](./tex/e0e88dba678ca3ead120b088f41191b2.png)