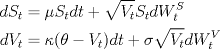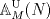 I2 Análisis Real, 2S 2009 |
|
|
|
|
|
|
Foro fmat.cl > Programa Enseñanza Universitaria > Comunidades Universitarias > Universidad Católica > Análisis Real  |
  Oct 5 2009, 09:05 PM
Publicado:
#1
|
|
 Dios Matemático Supremo  Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:   |
![TEX: \noindent \\<br />\begin{center}MAT2515 - Análisis Real\\<br />Interrogación II - Lunes 05 de Octubre de 2009\end{center}<br />\begin{enumerate}<br />\item Decidir si las siguientes afirmaciones son verdaderas o falsas. Si son falsas, dar contraejemplo.<br />\begin{enumerate}<br />\item Si $(X,d)$ es un espacio métrico arbitrario, y $A,B$ son abiertos conexos con intersección no vacía, entonces $A\cap B$ es conexo.<br />\item Sea $E=\left\{(x,y,z)\in\mathbb{R}^3/(x-1)^2+y^2+(z-2)^2\leq 1\right\}$ y $f:E\to\mathbb{R}$, continua y no constante, entonces existen $a,b\in\mathbb{R}$ con $a<b$ tal que $f(E)=[a,b]$.<br />\item Si $f:\mathbb{R}\to\mathbb{R}$ es continua y sobre entonces para todo conexo no vacío $E$ en $\mathbb{R},f^{-1}(E)$ es conexo.<br />\end{enumerate}<br />\item \begin{enumerate}<br />\item Sea $(X,d)$ un espacio métrico; sean $C$ y $D$ completos en $(X,D)$; demuestre que $C\cup D$ es completo.<br />\item Sea $X=\left\{f:[0,1]\to\mathbb{R} \text{ continuas}\right\}; d(f,g)=\displaystyle\int_0^1|f(x)-g(x)|dx$. Demuestre que $(X,d)$ no es completo.<br />\end{enumerate}<br />\item Sean $(X,d),(Y,\sigma)$ espacios métricos y $f:(X,d)\to(Y,\sigma)$ uniformemente continua.<br />\begin{enumerate}<br />\item Demuestre que si $(x_n)$ es de Cauchy en $(X,d)$ entonces $(f(x_n))$ es de Cauchy en $(Y,\sigma)$.<br />\item Dé un ejemplo de un espacio métrico $(X,d),$ y $f:(X,d)\to(X,d)$ continua para el cual se tenga una sucesión $(x_n)$ de Cauchy en $(X,d)$ y que $(f(x_n))$ no sea de Cauchy en $(X,d)$.<br />\end{enumerate}\end{enumerate}<br />](./tex/419e6feb2352a7dfa2c058ed0b6a37ce.png) ![TEX: \begin{enumerate}\item[$4.$] Sea \[X=\left\{f:[0,1]\to\mathbb{R}\text{ continuas}\right\}\qquad ; \qquad \delta(f,g)=\max_{x\in[0,1]} |f(x)-g(x)|\]<br />\[C=\left\{f\in X/\max_{x\in[0,1]}|f(x)|\leq 1\right\}\]\begin{enumerate}<br />\item Encuentre una sucesión $(f_n)\in C$ tal que $\delta(f_n,f_m)=1,$ si $n\not= m$.<br />\item Demuestre que si $P_1,\ldots,P_k$ es una colección finita de elementos de $C$ entonces $\displaystyle\bigcup_{i=1}^kB\left(P_i,\frac{1}{2}\right)$ no contiene a $C$.<br />\end{enumerate}\end{enumerate}](./tex/26939510215f99c7a9e106726cf61e6a.png)
-------------------- |
 |
 
|
![TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]](./tex/e0e88dba678ca3ead120b088f41191b2.png)
|
Oct 6 2009, 10:37 AM
Publicado:
#2
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad: Colegio/Liceo:  Sexo:  |
![TEX: $ $\\<br />Solucion a algunas del problema 1:\\<br />$ $\\<br />a) Correcto, consideramos la hipot\'etica existencia de $F:A\cup B\to\{0,1\}$ cont\'inua, por tanto sus restricciones a $A$ y $B$ son tambi\'en cont\'inua, sin embargo podemos pensar sin perder generalidad que $\exists x\in A\cap B$ tal que $F(x)=0$, y como $F^{-1}(\{1\})\subseteq A\cup B$ se concluye que hay al menos un $y\in A$ por ejemplo tal que $F(y)=1$, y por tanto la restricci\'on de $F$ a $A$ es cont\'inua, luego $A$ resultar\'ia ser no conexo.\\<br />$ $\\<br />b) Correcto, la im\'agen cont\'inua de un conexo es conexo, luego $f(E)$ es un intervalo; adem\'as $E$ es cerrado y acotado, luego es compacto y la im\'agen cont\'inua de compactos es compacto, luego $f(E)$ debes ser un intervalo compacto, o sea de la forma $[a,b]$. Finalmente como $f$ no es constante debe ser $a<b$.\\<br />$ $\\<br />c) sospecho que es falso, pero no se me ocurre contraejemplo.\\<br />$ $\\<br />](./tex/1ccdee53dfe2ffa53f52717f5389287f.png)
Mensaje modificado por Kaissa el Oct 6 2009, 10:38 AM -------------------- |
|
|
|
|
Oct 6 2009, 03:16 PM
Publicado:
#3
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad: Colegio/Liceo: Universidad: Sexo: |
Perdón, me equivoqué al tipear la 1a). Ahora está arreglado.
Para la 1c), la gracia es que f no tiene que ser inyectiva. -------------------- |
|
|
|
|
Oct 6 2009, 04:55 PM
Publicado:
#4
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad: Colegio/Liceo: Sexo: |
pero la 1c paso de ser entretenida a ser repetitiva po ¿estas seguro que preguntaban por la interseccion?? te lo digo porque vacio tambien es conexo, entonces es como exceso de hipotesis.
-------------------- |
|
|
|
|
Oct 6 2009, 05:54 PM
Publicado:
#5
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad: Colegio/Liceo: Universidad: Sexo: |
CITA(Kaissa @ Oct 6 2009, 05:55 PM)  pero la 1c paso de ser entretenida a ser repetitiva po ¿estas seguro que preguntaban por la interseccion?? te lo digo porque vacio tambien es conexo, entonces es como exceso de hipotesis. Si. Seguro. -------------------- |
|
|
|
|
Feb 12 2010, 08:02 PM
Publicado:
#6
|
|
 Staff FMAT  Grupo: Super Moderador Mensajes: 4.857 Registrado: 2-January 08 Miembro Nº: 14.268 Nacionalidad: Colegio/Liceo:  Universidad:  Sexo: |
![TEX: % MathType!MTEF!2!1!+-<br />% feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaadaqjEa<br />% qaaiaabofacaqGqbGaae4maiaab6cacaqGbbaaaaqaaiaabcfacaqG<br />% VbGaaeOCaiaabccacaqGKbGaaeyzaiaab2gacaqGVbGaae4Caiaabs<br />% hacaqGYbGaaeyyaiaabkhacaqGSaGaaeiiaiaabccadaGadaqaaiaa<br />% dAgadaqadaqaaiaadIhadaWgaaWcbaGaamOBaaqabaaakiaawIcaca<br />% GLPaaaaiaawUhacaGL9baacaqGGaGaaeyzaiaabohacaqGGaGaaeiz<br />% aiaabwgacaqGGaGaae4yaiaabggacaqG1bGaae4yaiaabIgacaqG5b<br />% GaaeOlaaqaamaaL4babaGaaeiraiaabwgacaqGTbGaae4Baiaaboha<br />% caqG0bGaaeOCaiaabggacaqGJbGaaeyAaiaab+gacaqGUbGaaeiiai<br />% aabQdaaaaabaGaaeiraiaabggacaqGKbGaae4BaiaabccacaqGXbGa<br />% aeyDaiaabwgacaqGGaWaaiWaaeaacaWG4bWaaSbaaSqaaiaad6gaae<br />% qaaaGccaGL7bGaayzFaaGaaeiiaiaabwgacaqGZbGaaeiiaiaabsga<br />% caqGLbGaaeiiaiaabogacaqGHbGaaeyDaiaabogacaqGObGaaeyEai<br />% aabYcacaqGGaGaae4CaiaabwgacaqGGaGaaeiDaiaabMgacaqGLbGa<br />% aeOBaiaabwgacaqGGaGaaeiiaiaadsgadaqadaqaaiaadIhadaWgaa<br />% WcbaGaamOBaaqabaGccaGGSaGaamiEamaaBaaaleaacaWGTbaabeaa<br />% aOGaayjkaiaawMcaaiabgYda8iabew9aMjaabccacaqGGaGaaeiCai<br />% aabggacaqGYbGaaeyyaiaabccacaqGJbGaaeyDaiaabggacaqGSbGa<br />% aeyCaiaabwhacaqGPbGaaeyzaiaabkhacaqGGaGaaeiiaiabew9aMj<br />% abg6da+iaaicdacaqGGaGaaeyEaiaabccacaqGNbGaaeyyaiaabkha<br />% caqGHbGaaeOBaiaabshacaqGPbGaaeOEaiaabggacaqGUbGaaeizai<br />% aab+gaaeaacaqGSbGaaeyyaiaabccacaqGLbGaaeiEaiaabMgacaqG<br />% ZbGaaeiDaiaabwgacaqGUbGaae4yaiaabMgacaqGHbGaaeiiaiaabs<br />% gacaqGLbGaaeiiaiaabccacaWGobGaeyicI4SaeSyfHuQaaeiiaiaa<br />% bshacaqGHbGaaeiBaiaabccacaqGXbGaaeyDaiaabwgacaqGGaGaae<br />% iiaiaad6gacaGGSaGaamyBaiabg6da+iaad6eacaqGUaGaaeiiaiaa<br />% bYeacaqG1bGaaeyzaiaabEgacaqGVbGaaeilaiaabccacaqGZbGaae<br />% yAaiaabwgacaqGUbGaaeizaiaab+gacaqGGaGaaeiiaiaadAgacaqG<br />% GaGaaeyDaiaab6gacaqGPbGaaeOzaiaab+gacaqGYbGaaeyBaiaabw<br />% gacaqGTbGaaeyzaiaab6gacaqG0bGaaeyzaiaabccacaqGJbGaae4B<br />% aiaab6gacaqG0bGaaeyAaiaab6gacaqG1bGaaeyyaiaabccacaqGZb<br />% GaaeyzaiaabccacaqGZbGaaeyAaiaabEgacaqG1bGaaeyzaaqaaiaa<br />% bghacaqG1bGaaeyzaiaabccacaqGGaGaeq4Wdm3aaeWaaeaacaWGMb<br />% WaaeWaaeaacaWG4bWaaSbaaSqaaiaad6gaaeqaaaGccaGLOaGaayzk<br />% aaGaaiilaiaadAgadaqadaqaaiaadIhadaWgaaWcbaGaamyBaaqaba<br />% aakiaawIcacaGLPaaaaiaawIcacaGLPaaacqGH8aapcqaH1oqzcaqG<br />% GaGaaeilaiaabccacqGHaiIicqaH1oqzcqGH+aGpcaaIWaGaaiOlai<br />% aabccaaeaaaeaacaqGqbGaae4BaiaabkhacaqGGaGaaeiBaiaab+ga<br />% caqGGaGaaeiDaiaabggacaqGUbGaaeiDaiaab+gacaqGSaGaaeiiai<br />% aabccacqGHaiIicqaH1oqzcqGH+aGpcaaIWaGaaeiiaiaabMhacaqG<br />% GaGaaeizaiaabggacaqGKbGaae4BaiaabccacaqGGaGaamOtaiabgI<br />% GiolablwriLkaabccacaqG0bGaaeyyaiaabYgacaqGGaGaaeyCaiaa<br />% bwhacaqGLbGaaeiiaiaabccacaWGUbGaaiilaiaad2gacqGH+aGpca<br />% WGobGaaeiiaiaabohacaqGLbGaaeiiaiaabshacaqGPbGaaeyzaiaa<br />% b6gacaqGLbGaaeiiaiabeo8aZnaabmaabaGaamOzamaabmaabaGaam<br />% iEamaaBaaaleaacaWGUbaabeaaaOGaayjkaiaawMcaaiaacYcacaWG<br />% MbWaaeWaaeaacaWG4bWaaSbaaSqaaiaad2gaaeqaaaGccaGLOaGaay<br />% zkaaaacaGLOaGaayzkaaGaeyipaWJaeqyTduMaaeilaiaabccacaqG<br />% LbGaae4CaiaabccacaqGKbGaaeyzaiaabogacaqGPbGaaeOCaaqaam<br />% aacmaabaGaamOzamaabmaabaGaamiEamaaBaaaleaacaWGUbaabeaa<br />% aOGaayjkaiaawMcaaaGaay5Eaiaaw2haaiaabccacaqGLbGaae4Cai<br />% aabccacaqGKbGaaeyzaiaabccacaqGJbGaaeyyaiaabwhacaqGJbGa<br />% aeiAaiaabMhacaqGUaaaaaa!7502!<br />\[<br />\begin{gathered}<br /> \boxed{{\text{SP3}}{\text{.A}}} \hfill \\<br /> {\text{Por demostrar}}{\text{, }}\left\{ {f\left( {x_n } \right)} \right\}{\text{ es de cauchy}}{\text{.}} \hfill \\<br /> \boxed{{\text{Demostracion :}}} \hfill \\<br /> {\text{Dado que }}\left\{ {x_n } \right\}{\text{ es de cauchy}}{\text{, se tiene }}d\left( {x_n ,x_m } \right) < \varphi {\text{ para cualquier }}\varphi > 0{\text{ y garantizando}} \hfill \\<br /> {\text{la existencia de }}N \in \mathbb{N}{\text{ tal que }}n,m > N{\text{. Luego}}{\text{, siendo }}f{\text{ uniformemente continua se sigue}} \hfill \\<br /> {\text{que }}\sigma \left( {f\left( {x_n } \right),f\left( {x_m } \right)} \right) < \varepsilon {\text{ }}{\text{, }}\forall \varepsilon > 0.{\text{ }} \hfill \\<br /> \hfill \\<br /> {\text{Por lo tanto}}{\text{, }}\forall \varepsilon > 0{\text{ y dado }}N \in \mathbb{N}{\text{ tal que }}n,m > N{\text{ se tiene }}\sigma \left( {f\left( {x_n } \right),f\left( {x_m } \right)} \right) < \varepsilon {\text{, es decir}} \hfill \\<br /> \left\{ {f\left( {x_n } \right)} \right\}{\text{ es de cauchy}}{\text{.}} \hfill \\ <br />\end{gathered} <br />\]](./tex/4fb348f8fa7d17ec89ec1751bd20a878.png) -------------------- Candidato a doctor en Cs. De la ingeniería mención modelamiento matemático, DIM. Universidad de Chile
Magíster en ciencias mención matemática, Profesor de estado en matemáticas y computación, Licenciado en educación matemáticas y computación, USACH |
|
|
|
|
Feb 15 2010, 02:57 PM
Publicado:
#7
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 560 Registrado: 24-December 09 Miembro Nº: 64.629 |
Problema 1.c
Es falsa, contraejemplo: Sea ![TEX: $E=(0,1]$](./tex/aeaaad194f060310b7723e9331025941.png) y 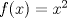 . Luego se tiene que ![TEX: $f^{-1}(E)=[-1,1]\setminus \{0\}$](./tex/672a1fd9ceb98c2ae207bd7837127da5.png) el cual no es conexo.
Mensaje modificado por aleph_omega el Feb 15 2010, 03:00 PM |
|
|
|
|
Mar 3 2010, 09:11 PM
Publicado:
#8
|
|
|
Staff FMAT Grupo: Super Moderador Mensajes: 4.857 Registrado: 2-January 08 Miembro Nº: 14.268 Nacionalidad: Colegio/Liceo: Universidad: Sexo: |
![TEX: % MathType!MTEF!2!1!+-<br />% feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaadaqjEa<br />% qaaiaabofacaqGqbGaaeOmaaaaaeaacaWGHbGaaiykaiaaboeacaqG<br />% VbGaaeOBaiaabohacaqGPbGaaeizaiaabwgacaqGYbGaaeyzaiaab2<br />% gacaqGVbGaae4CaiaabccacaqGSbGaaeyyaiaabccacaqGZbGaaeyD<br />% aiaabogacaqGLbGaae4CaiaabMgacaqGVbGaaeOBaiaabccadaGada<br />% qaaiaadIhadaWgaaWcbaGaamOBaaqabaaakiaawUhacaGL9baacaqG<br />% GaGaaeizaiaabwgacaqGGaGaae4yaiaabggacaqG1bGaae4yaiaabI<br />% gacaqG5bGaaeiiaiaabwgacaqGUbGaaeiiaiaabccacaWGdbGaeyOk<br />% IGSaamiraiaabYcacaqGGaGaaeiBaiaabwhacaqGLbGaae4zaiaab+<br />% gacaqGGaGaaeizaiaabMgacaqGJbGaaeiAaiaabggacaqGGaGaae4C<br />% aiaabwhacaqGJbGaaeyzaiaabohacaqGPbGaae4Baiaab6gacaqGGa<br />% GaaeODaiaabMgacaqG2bGaaeyzaiaabccacaqGLbGaaeOBaaqaaiaa<br />% doeacaqGGaGaae4BaiaabccacaqGLbGaaeOBaiaabccacaWGebGaae<br />% OlaiaabccacaqGtbGaaeyAaiaabccacaqGKbGaaeyAaiaabogacaqG<br />% ObGaaeyyaiaabccacaqGZbGaaeyDaiaabogacaqGLbGaae4yaiaabM<br />% gacaqGVbGaaeOBaiaabccacaqGKbGaaeyzaiaabccacaqGJbGaaeyy<br />% aiaabwhacaqGJbGaaeiAaiaabMhacaqGGaGaaeODaiaabMgacaqG2b<br />% GaaeyzaiaabccacaqGLbGaaeOBaiaabccacaWGdbGaaeilaiaabcca<br />% caqGLbGaae4CaiaabccacaqGJbGaae4Baiaab6gacaqG2bGaaeyzai<br />% aabkhacaqGNbGaaeyzaiaab6gacaqG0bGaaeyzaiaabccacaqGHbGa<br />% aeiiaiaabwhacaqGUbGaaeiiaiaabchacaqG1bGaaeOBaiaabshaca<br />% qGVbGaaeiiaiaabsgacaqGLbGaaeiiaiaabwgacaqGZbGaaeiDaiaa<br />% bwgacaqGGaGaaeiCaiaab+gacaqGYbaabaGaaeiBaiaabggacaqGGa<br />% Gaae4yaiaab+gacaqGTbGaaeiCaiaabYgacaqGLbGaaeiDaiaabMga<br />% caqG0bGaaeyDaiaabsgacaqGGaGaaeizaiaabwgacaqGGaGaae4qai<br />% aabYcacaqGGaGaaeyyaiaab6gacaqGHbGaaeiBaiaab+gacaqGNbGa<br />% ae4BaiaabccacaqGWbGaaeyyaiaabkhacaqGHbGaaeiiaiaabseaca<br />% qGUaGaaeiiaiaabYeacaqG1bGaaeyzaiaabEgacaqGVbGaaeiiaiaa<br />% bYgacaqGHbGaaeiiaiaabwhacaqGUbGaaeyAaiaab+gacaqGUbGaae<br />% iiaiaabsgacaqGLbGaaeiiaiaabogacaqGVbGaaeyBaiaabchacaqG<br />% SbGaaeyzaiaabshacaqGVbGaae4CaiaabccacaqGLbGaae4Caiaabc<br />% cacaqGJbGaae4Baiaab2gacaqGWbGaaeiBaiaabwgacaqG0bGaae4B<br />% aiaab6caaaaa!0AAC!<br />\[<br />\begin{gathered}<br /> \boxed{{\text{SP2}}} \hfill \\<br /> a){\text{Consideremos la sucesion }}\left\{ {x_n } \right\}{\text{ de cauchy en }}C \cup D{\text{, luego dicha sucesion vive en}} \hfill \\<br /> C{\text{ o en }}D{\text{. Si dicha sucecion de cauchy vive en }}C{\text{, es convergente a un punto de este por}} \hfill \\<br /> {\text{la completitud de C}}{\text{, analogo para D}}{\text{. Luego la union de completos es completo}}{\text{.}} \hfill \\ <br />\end{gathered} <br />\]](./tex/eab5bb53288c544f11b18fa7860a2ab7.png) -------------------- Candidato a doctor en Cs. De la ingeniería mención modelamiento matemático, DIM. Universidad de Chile
Magíster en ciencias mención matemática, Profesor de estado en matemáticas y computación, Licenciado en educación matemáticas y computación, USACH |
|
|
|
|
Mar 3 2010, 09:25 PM
Publicado:
#9
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.818 Registrado: 21-December 06 Miembro Nº: 3.434 |
CITA(Uchiha Itachi @ Mar 3 2010, 10:11 PM) El principio de la demostración está mal, porque la sucesión puede tener términos tanto en C como en D, no sólo en uno de los 2 conjuntos. -------------------- |
|
|
|
|
Mar 3 2010, 10:29 PM
Publicado:
#10
|
|
|
Staff FMAT Grupo: Super Moderador Mensajes: 4.857 Registrado: 2-January 08 Miembro Nº: 14.268 Nacionalidad: Colegio/Liceo: Universidad: Sexo: |
CITA(DressedToKill @ Mar 4 2010, 02:25 AM) El principio de la demostración está mal, porque la sucesión puede tener términos tanto en C como en D, no sólo en uno de los 2 conjuntos. Siiii  , despues me puse a pensar que los elementos de la sucesion podian vivir en C o en D, no necesariamente la sucesion... a seguir intentando
-------------------- Candidato a doctor en Cs. De la ingeniería mención modelamiento matemático, DIM. Universidad de Chile
Magíster en ciencias mención matemática, Profesor de estado en matemáticas y computación, Licenciado en educación matemáticas y computación, USACH |
|
|
|
|
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 1st May 2025 - 03:04 AM |
