Final Nacional Nivel Mayor 2009 - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Sector Preparación Olimpiadas > Competencias y Olimpiadas > Olimpiadas > Olimpiada Nacional

4 Páginas:

1 2 3 > »

Reply to this topic

Start new topic

Final Nacional Nivel Mayor 2009

~Fatal_Collapse~ Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 23 2009, 04:24 PM Publicado: #1
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	XXI OLIMPIADA NACIONAL DE MATEMÁTICAS Prueba Final, Nivel Mayor Primera parte, Lunes 23 de noviembre de 2009 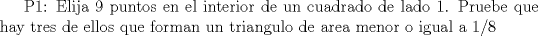$TEX: P1: Elija $9$ puntos en el interior de un cuadrado de lado $1$. Pruebe que hay tres de ellos que forman un triangulo de area menor o igual a $1/8$$ $TEX: P2: Considere $P$ un poligono regular convexo de 9 lados con cada lado de longitud $1$. Una diagonal en $P$ es cualquier trazo que une dos vertices no adyacentes de $P$. Calcule la diferencia entre las longitudes de la mayor y menor diagonal de $P$$ $TEX: P3: Se construye la suma siguiente:<br /><br />$S=\dfrac {1}{a_1}+\dfrac{2}{a_2}+...+\dfrac{100}{a_{100}}$<br /><br />Donde $a_1, a_2,..., a_{100}$ son numeros enteros positivos. ¿Cuales son todos los posibles valores enteros que puede tomar $S$?$ Segunda parte, Martes 24 de noviembre de 2009 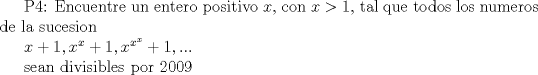$TEX: P4: Encuentre un entero positivo $x$, con $x>1$, tal que todos los numeros de la sucesion<br /><br />$x+1, x^x+1, x^{x^x}+1,...$<br /><br />sean divisibles por $2009$$ $TEX: P5: Sean $A$ y $B$ dos cubos. Se asignan los numeros $1,2,...,14$ en cualquier orden, a las caras y a los vertices del cubo. Luego se asigna a cada arista del cubo $A$ el promedio de los numeros asignados a las dos caras que la contienen. Finalmente se asigna a cada cara del cubo $B$ la suma de los numeros asociados a los vertices, la cara y las aristas en la cara correspondiente del cubo $A$. Si $S$ es la suma de los numeros asignados a las caras de $B$, encuentre el maximo y el minimo valor que puede tomar $S$.$ $TEX: P6. Se tienen $n\ge 6$ puntos verdes en el plano, tal que no hay $3$ de ellos colineales. Suponga ademas que $6$ de estos puntos son los vertices de un hexagono convexo. Demuestre que existen $5$ puntos verdes que forman un pentagono que no contiene otro punto verde en su interior.$ -------------------- Ricardo Vargas Obando Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile. Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico: Medalla de Plata, XIX Olimpiada Nacional de Matemática Nivel Menor (2007) Medalla de Oro, XXI Olimpiada Nacional de Matemática Nivel Mayor (2009) Medalla de Bronce, XXV Olimpiada Iberoamericana de Matemática (2010) Medalla de Oro, XXII Olimpiada Nacional de Matemática Nivel Mayor (2010) "What we learned as children, that one plus one equals two, we know to be false. One plus one equals one. We even have a word when you plus another, equals one. That word is love." "Todos piensan en cambiar el mundo, pero nadie piensa en cambiarse a sí mismo."

~Fatal_Collapse~ Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 23 2009, 05:38 PM Publicado: #2
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Problema 1: $TEX: Sean $A,B,C,D$ los vertices del cuadrado unitario. Llamemos $E,F,G,H$ a los puntos medios de $AB, BC,CD,DA$, respectivamente, y sea $O$ el centro del cuadrado. Considerando los cuatro cuadrados $AEOH, EOFB, OFCG, OGDH$, y los 9 puntos al interior del cuadrado $ABCD$, tenemos que por el principio del palomar, hay al menos 3 puntos dentro de un mismo cuadrado señalado. Sean $P_1, P_2, P_3$ tres de esos puntos. Solo nos resta probar que $S_{P_1P_2P_3}\leq \dfrac{1}{8}$, donde $S_{P_1P_2P_3}$ denota el area del $\triangle P_1P_2P_3$, lo cual es un caso particular de una generalizacion adecuada del problema 2 de la final del nivel menor considerando el cuadrado adecuado.$ -------------------- Ricardo Vargas Obando Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile. Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico: Medalla de Plata, XIX Olimpiada Nacional de Matemática Nivel Menor (2007) Medalla de Oro, XXI Olimpiada Nacional de Matemática Nivel Mayor (2009) Medalla de Bronce, XXV Olimpiada Iberoamericana de Matemática (2010) Medalla de Oro, XXII Olimpiada Nacional de Matemática Nivel Mayor (2010) "What we learned as children, that one plus one equals two, we know to be false. One plus one equals one. We even have a word when you plus another, equals one. That word is love." "Todos piensan en cambiar el mundo, pero nadie piensa en cambiarse a sí mismo."

Newtype Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 23 2009, 05:42 PM Publicado: #3
Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 1.559 Registrado: 18-November 07 Miembro Nº: 12.754 Nacionalidad: Sexo:	wow!! felicidades Kain ojala te haya ido excelente hoy! y a losdemasde fmat tambien! Viendo el 1. cache que era con principio del palomar pero nose me ocurrio esa distribucion inteligente..es fruto de tu talento y entrenamiento! exito mañana y una medallita ojala -------------------- Empezando con Desigualdades? Encuentra aquí problemas resueltos

Infinite Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 23 2009, 07:01 PM Publicado: #4
Puntaje Nacional PSU Matemáticas Admisión 2010 Grupo: Usuario FMAT Mensajes: 99 Registrado: 2-March 08 Miembro Nº: 16.121 Nacionalidad: Sexo:	Dibujo.JPG ( 24.26k ) Número de descargas: 26 ABCD es ciclico, luego por Ptolomeo ACBD=ABDC+AD*BC pero AC=AD=DC y AB=1 luego BD-AC=1 PD: Sorry por el dibujo

~Fatal_Collapse~ Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 23 2009, 09:31 PM Publicado: #5
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	La solucion de Infinite al problema 2 es correcta =), corta y precisa. A decir verdad he visto demasiadas soluciones de este problema aca con los cabros. Aca posteo una breve reseña de las distintas soluciones: Aplique trigonometria y tres veces el teo del coseno Aplique Teorema de Ptolomeo dos veces, teo del coseno y forme sistemas de ecuaciones (cuando tenga tiempo libre posteo esta solucion que fue la que ocupe) Una de las diagonales menores prolonguela en un segmento de medida 1, forme isosceles y concluya (tambien se me ocurrio hacer eso en la prueba) Considere las novenas raices de la unidad en el plano complejo Ponga el poligono en un plano cartesiano Forme trapecios adecuados (si makmat tiene ocasion de explicar su solucion, bienvenido sea) Forme equilateros adecuados (si Kenshin tiene ocasion de explicarlo como lo hizo en el CPEIP, bienvenido sea Como hizo Infinite, una simple aplicacion del Teo De Ptolomeo funciona de maravillas Muchas formas para resolver un solo problema como pueden ver. Saludos -------------------- Ricardo Vargas Obando Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile. Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico: Medalla de Plata, XIX Olimpiada Nacional de Matemática Nivel Menor (2007) Medalla de Oro, XXI Olimpiada Nacional de Matemática Nivel Mayor (2009) Medalla de Bronce, XXV Olimpiada Iberoamericana de Matemática (2010) Medalla de Oro, XXII Olimpiada Nacional de Matemática Nivel Mayor (2010) "What we learned as children, that one plus one equals two, we know to be false. One plus one equals one. We even have a word when you plus another, equals one. That word is love." "Todos piensan en cambiar el mundo, pero nadie piensa en cambiarse a sí mismo."

xD13G0x Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 23 2009, 11:05 PM Publicado: #6
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 532 Registrado: 19-October 08 Desde: Santa Cruz de la Sierra Miembro Nº: 36.531 Nacionalidad: Sexo:	Primero quisiera preguntar algunas cosas: -Cuanto dura la prueba -Los problemas estan ordenados por orden de dificultad (segun el jurado, segun yo puede ser lo contrario) -Cuando dan la segunda parte Bueno ahora. Solucion problema 3: 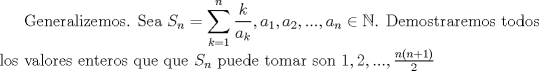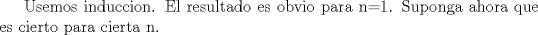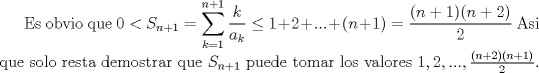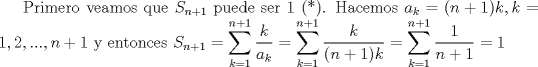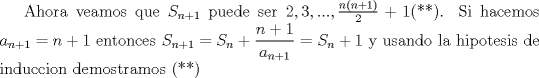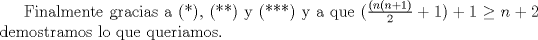$TEX: Generalizemos. Sea $S_n=\displaystyle \sum_{k=1}^{n} \dfrac {k}{a_k},a_1,a_2,...,a_n \in \mathbb{N}$. Demostraremos todos los valores enteros que que $S_n$ puede tomar son $1,2,..., \frac{n(n+1)}{2}$$ $TEX: Usemos induccion. El resultado es obvio para n=1. Suponga ahora que es cierto para cierta n.$ $TEX: Es obvio que $0 < S_{n+1}=\displaystyle \sum_{k=1}^{n+1} \dfrac {k}{a_k} \le 1+2+...+(n+1)= \dfrac{(n+1)(n+2)}{2}$ Asi que solo resta demostrar que $S_{n+1}$ puede tomar los valores $1,2,..., \frac{(n+2)(n+1)}{2}$.$ $TEX: Primero veamos que $S_{n+1}$ puede ser 1 (). Hacemos $a_k=(n+1)k, k=1,2,...,n+1$ y entonces $S_{n+1}=\displaystyle \sum_{k=1}^{n+1} \dfrac {k}{a_k}= \displaystyle \sum_{k=1}^{n+1} \dfrac {k}{(n+1)k}= \displaystyle \sum_{k=1}^{n+1} \dfrac {1}{n+1}=1$$ $TEX: Ahora veamos que $S_{n+1}$ puede ser $2,3,...,\frac{n(n+1)}{2}+1$(). Si hacemos $a_{n+1}=n+1$ entonces $S_{n+1}=S_n+ \dfrac{n+1}{a_{n+1}}=S_n+1$ y usando la hipotesis de induccion demostramos ()$ $TEX: Ahora veamos que $S_{n+1}$ puede ser $n+2,n+3,...,\frac{n(n+1)}{2}+n+1= \frac{(n+1)(n+2)}{2}$() Hacemos $a_{n+1}=1$ entonces $S_{n+1}=S_n+ \dfrac{n+1}{a_{n+1}}=S_n+n+1$ y usando la hipotesis de induccion demostramos ().$ $TEX: Finalmente gracias a (), () y () y a que $(\frac {(n(n+1)}{2}+1)+1 \ge n+2$ demostramos lo que queriamos.$ Mensaje modificado por xD13G0x* el Nov 24 2009, 11:33 AM -------------------- "I've never let my school interfere with my education.”

~Fatal_Collapse~ Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 24 2009, 05:06 AM Publicado: #7
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Respondiendo a tus preguntas Diego, la prueba duraba 3 horas, y aparentemente estan por orden de dificultad (en realidad los que rendimos la prueba no lo sabemos, pero como tu señalas, eso es relativo al sujeto cognoscente), y hoy dia damos la segunda parte, y si puedo la subo o me aprovecho de alguien que la suba xD. La solucion al p3 la reviso cuando tenga mas tiempo, pero puedo ver que por lo menos llegaste al mismo resultado que yo en la prueba, y muchos llegaron al resultado, pero lo dificil era formalizarlo (por lo menos ahi chamulle como muchos xD). Saludos -------------------- Ricardo Vargas Obando Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile. Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico: Medalla de Plata, XIX Olimpiada Nacional de Matemática Nivel Menor (2007) Medalla de Oro, XXI Olimpiada Nacional de Matemática Nivel Mayor (2009) Medalla de Bronce, XXV Olimpiada Iberoamericana de Matemática (2010) Medalla de Oro, XXII Olimpiada Nacional de Matemática Nivel Mayor (2010) "What we learned as children, that one plus one equals two, we know to be false. One plus one equals one. We even have a word when you plus another, equals one. That word is love." "Todos piensan en cambiar el mundo, pero nadie piensa en cambiarse a sí mismo."

~Fatal_Collapse~ Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 24 2009, 12:12 PM Publicado: #8
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Solucion al problema 4: $TEX: Por comodidad definamos la secuencia $a_n$ como $a_1=x$ y $a_{n+1}=x^{a_n}$. Primero que nada por la condicion del problema $a_1\equiv -1\pmod {2009}$ y luego $a_{n+1}\equiv (-1)^{a_n}\pmod {2009}$. Nos piden que $\forall n\in \mathbb{Z}^+$ se cumpla que $a_n\equiv -1\pmod {2009}$, y para eso se debe cumplir que todos los $a_n$ sean impares, en particular el que nos interesa, $a_1$. Entonces como $a_1$ es de la forma $2009j-1$ (con j entero positivo), y es impar, se tiene que $2009j$ debe ser par, y por ende, $x$ es de la forma $4018k-1$, con $k\in \mathbb{Z}^+$. Con esto obtenemos infinitos valores de $x$, es mas, tomando $k=1$ se tiene que $x=4017$ satisface lo pedido.$ -------------------- Ricardo Vargas Obando Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile. Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico: Medalla de Plata, XIX Olimpiada Nacional de Matemática Nivel Menor (2007) Medalla de Oro, XXI Olimpiada Nacional de Matemática Nivel Mayor (2009) Medalla de Bronce, XXV Olimpiada Iberoamericana de Matemática (2010) Medalla de Oro, XXII Olimpiada Nacional de Matemática Nivel Mayor (2010) "What we learned as children, that one plus one equals two, we know to be false. One plus one equals one. We even have a word when you plus another, equals one. That word is love." "Todos piensan en cambiar el mundo, pero nadie piensa en cambiarse a sí mismo."

xD13G0x Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 24 2009, 01:50 PM Publicado: #9
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 532 Registrado: 19-October 08 Desde: Santa Cruz de la Sierra Miembro Nº: 36.531 Nacionalidad: Sexo:	el problema 6 supongo que sale induciendo, desmotrando que si tenemos un punto en el interior de un pentagono (convexo o concavo) podemos encontrar un pentagono con vertices en los 6 puntos que no contiene el otro punto que no esta en el pentagono. intente hacer esto triangulizando el pentagono, pero no estoy seguro de lo que hize -------------------- "I've never let my school interfere with my education.”

Newtype Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 24 2009, 02:35 PM Publicado: #10
Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 1.559 Registrado: 18-November 07 Miembro Nº: 12.754 Nacionalidad: Sexo:	Hola 2 dudas: 1. Al apoyarnos en algun resultado prrevio, por eje,plo en este caso, el teorema de ptolomeo,debemos demostrar ese teorema, o enunciarlo, o lo podemos usar nomas y decir "por el teorema X" ? 2. CITA(Kain #13 @ Nov 23 2009, 10:31 PM) []Considere las novenas raices de la unidad en el plano complejo Pq las raices novenas? me intereso esto salu2 -------------------- Empezando con Desigualdades? Encuentra aquí problemas resueltos*

« Posterior · Olimpiada Nacional · Anterior »

4 Páginas:

1 2 3 > »

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 16th June 2025 - 08:33 AM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.