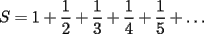Congruencia Modulo - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Sector Preparación Olimpiadas > Sector Olímpico > Teoría de Números > Material de Entrenamiento

3 Páginas:

< 1 2 3

Reply to this topic

Start new topic

Congruencia Modulo, Cuarta Parte(Problemas Propuestos)

Guía Rojo Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 22 2006, 01:32 PM Publicado: #21
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 903 Registrado: 28-May 05 Desde: Santiago, Chile Miembro Nº: 69 Nacionalidad: Colegio/Liceo: Sexo:	CITA Por inspección, resuelva las siguientes congruencias: 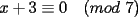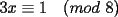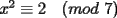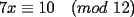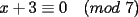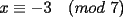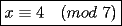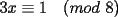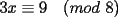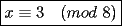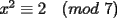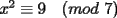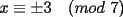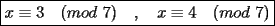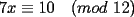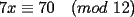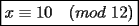$TEX: $x+3\equiv 0\ \ \ (mod\ 7)$$ $TEX: $3x\equiv 1\ \ \ (mod\ 8)$$ $TEX: $x^2\equiv 2\ \ \ (mod\ 7)$$ $TEX: $7x\equiv 10\ \ \ (mod\ 12)$$ $TEX: $x+3\equiv 0\ \ \ (mod\ 7)$$ $TEX: $x\equiv -3\ \ \ (mod\ 7)$$ $TEX: $\boxed{x\equiv 4\ \ \ (mod\ 7)}$$ $TEX: $3x\equiv 1\ \ \ (mod\ 8)$$ $TEX: $3x\equiv 9\ \ \ (mod\ 8)$$ $TEX: $\boxed{x\equiv 3\ \ \ (mod\ 8)}$$ $TEX: $x^2\equiv 2\ \ \ (mod\ 7)$$ $TEX: $x^2\equiv 9\ \ \ (mod\ 7)$$ $TEX: $x\equiv \pm 3\ \ \ (mod\ 7)$$ $TEX: $\boxed{x\equiv 3\ \ \ (mod\ 7)\ \ \ ,\ \ \ x\equiv 4\ \ \ (mod\ 7)}$$ $TEX: $7x\equiv 10\ \ \ (mod\ 12)$$ $TEX: $7x\equiv 70\ \ \ (mod\ 12)$$ $TEX: $\boxed{x\equiv 10\ \ \ (mod\ 12)}$$ -------------------- Bachiller en Ciencias (ex) Estudiante de Medicina Estudiante de Ingeniería Civil de Industrias, diploma en Ingeniería Matemática Pontificia Universidad Católica de Chile "El espíritu del matemático busca la belleza del pensamiento, y esa va de la mano con la filosofía." - Héctor Hardy Pastén Vásquez "¿Qué te hace pensar que si tienes dos elementos de un conjunto con otros dos elementos de otro conjunto se origina uno nuevo con cuatro? Es sólo el sentido común, no te imaginas que los elementos aparecen de la nada, pero resulta que con el sólo hecho de cuestionar el sentido común, se podría afirmar que cuando juntas cuatro elementos aparecen miles de elementos más. Y si lo demuestras, todo se basa en la razón." - Alonso Duque Vega, razonador por excelencia $TEX: $S=1+dfrac{1}{2}+dfrac{1}{3}+dfrac{1}{4}+dfrac{1}{5}+ldots$$ Esta serie converge! He encontrado una maravillosa demostración de esto, pero no cabe en la estrechez de esta firma...

Guía Rojo Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 22 2006, 01:46 PM Publicado: #22
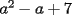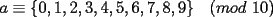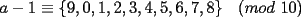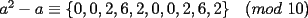Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 903 Registrado: 28-May 05 Desde: Santiago, Chile Miembro Nº: 69 Nacionalidad: Colegio/Liceo: Sexo:	CITA Para todo entero $TEX: $a$$ , muestre que $TEX: $a^2-a+7$$ termina en uno de los dígitos 3, 7 ó 9. 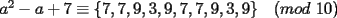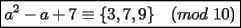$TEX: $a\equiv \{0,1,2,3,4,5,6,7,8,9\}\ \ \ (mod\ 10)$$ $TEX: $a-1\equiv \{9,0,1,2,3,4,5,6,7,8\}\ \ \ (mod\ 10)$$ $TEX: $a^2-a\equiv \{0,0,2,6,2,0,0,2,6,2\}\ \ \ (mod\ 10)$$ $TEX: $a^2-a+7\equiv \{7,7,9,3,9,7,7,9,3,9\}\ \ \ (mod\ 10)$$ $TEX: $\boxed{a^2-a+7\equiv \{3,7,9\}\ \ \ (mod\ 10)}$$ -------------------- Bachiller en Ciencias (ex) Estudiante de Medicina Estudiante de Ingeniería Civil de Industrias, diploma en Ingeniería Matemática Pontificia Universidad Católica de Chile "El espíritu del matemático busca la belleza del pensamiento, y esa va de la mano con la filosofía." - Héctor Hardy Pastén Vásquez "¿Qué te hace pensar que si tienes dos elementos de un conjunto con otros dos elementos de otro conjunto se origina uno nuevo con cuatro? Es sólo el sentido común, no te imaginas que los elementos aparecen de la nada, pero resulta que con el sólo hecho de cuestionar el sentido común, se podría afirmar que cuando juntas cuatro elementos aparecen miles de elementos más. Y si lo demuestras, todo se basa en la razón." - Alonso Duque Vega, razonador por excelencia $TEX: $S=1+dfrac{1}{2}+dfrac{1}{3}+dfrac{1}{4}+dfrac{1}{5}+ldots$$ Esta serie converge! He encontrado una maravillosa demostración de esto, pero no cabe en la estrechez de esta firma...

Guía Rojo Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 22 2006, 02:51 PM Publicado: #23
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 903 Registrado: 28-May 05 Desde: Santiago, Chile Miembro Nº: 69 Nacionalidad: Colegio/Liceo: Sexo:	CITA Asumiendo que 495 divide a 273x49y5, encuentre los dígitos x e y. Nota: 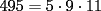$TEX: $495=5\cdot 9\cdot 11$$ 273x49y5 debe ser divisible por 9, cuya regla de divisibilidad es que la suma de sus dígitos sea un múltiplo de 9... luego, 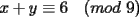$TEX: $x+y\equiv 6\ \ \ (mod\ 9)$$ los números buscados entonces podrían ser: (0,6) (1,5) (2,4) (3,3) (4,2) (5,1) (6,0) (6,9) (7,8) (8,7) (9,6) 273x49y5 debe ser divisible por 11, cuya regla de divisibilidad es que la diferencia entre las sumas de los dígitos alternados sea un múltiplo de 11... luego, 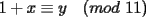$TEX: $1+x\equiv y\ \ \ (mod\ 11)$$ tenemos entonces un "sistema" de congruencias... 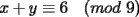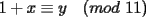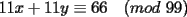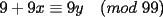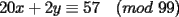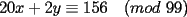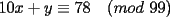$TEX: $x+y\equiv 6\ \ \ (mod\ 9)$$ $TEX: $1+x\equiv y\ \ \ (mod\ 11)$$ $TEX: $11x+11y\equiv 66\ \ \ (mod\ 99)$$ $TEX: $9+9x\equiv 9y\ \ \ (mod\ 99)$$ $TEX: $20x+2y\equiv 57\ \ \ (mod\ 99)$$ $TEX: $20x+2y\equiv 156\ \ \ (mod\ 99)$$ $TEX: $10x+y\equiv 78\ \ \ (mod\ 99)$$ como x e y son dígitos, la única manera de que se cumpla lo último dicho es que: 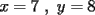$TEX: $x=7\ ,\ y=8$$ -------------------- Bachiller en Ciencias (ex) Estudiante de Medicina Estudiante de Ingeniería Civil de Industrias, diploma en Ingeniería Matemática Pontificia Universidad Católica de Chile "El espíritu del matemático busca la belleza del pensamiento, y esa va de la mano con la filosofía." - Héctor Hardy Pastén Vásquez "¿Qué te hace pensar que si tienes dos elementos de un conjunto con otros dos elementos de otro conjunto se origina uno nuevo con cuatro? Es sólo el sentido común, no te imaginas que los elementos aparecen de la nada, pero resulta que con el sólo hecho de cuestionar el sentido común, se podría afirmar que cuando juntas cuatro elementos aparecen miles de elementos más. Y si lo demuestras, todo se basa en la razón." - Alonso Duque Vega, razonador por excelencia $TEX: $S=1+dfrac{1}{2}+dfrac{1}{3}+dfrac{1}{4}+dfrac{1}{5}+ldots$$ Esta serie converge! He encontrado una maravillosa demostración de esto, pero no cabe en la estrechez de esta firma...

anti_seba Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 19 2010, 05:11 PM Publicado: #24
Principiante Matemático Grupo: Usuario FMAT Mensajes: 1 Registrado: 19-June 10 Miembro Nº: 72.902 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	No sé si sea el lugar mas adecuado pero estoy en serios problemas con este ejercicio: Probar que para todo n, n^7-n es divisible por 42. Alguein me ayude xfavor.

~Fatal_Collapse~ Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 19 2010, 05:17 PM Publicado: #25
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(anti_seba @ Jun 19 2010, 06:11 PM) No sé si sea el lugar mas adecuado pero estoy en serios problemas con este ejercicio: Probar que para todo n, n^7-n es divisible por 42. Alguein me ayude xfavor. Mediante congruencias? Nota que 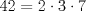$TEX: $42=2\cdot 3 \cdot 7$$ . 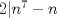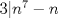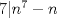Prueba que $TEX: $2\|n^7-n$$ , $TEX: $3\|n^7-n$$ y $TEX: $7\|n^7-n$$ y concluye (si quieres puedes ocupar el Pequeño Teorema de Fermat ) -------------------- Ricardo Vargas Obando Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile. Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico: Medalla de Plata, XIX Olimpiada Nacional de Matemática Nivel Menor (2007) Medalla de Oro, XXI Olimpiada Nacional de Matemática Nivel Mayor (2009) Medalla de Bronce, XXV Olimpiada Iberoamericana de Matemática (2010) Medalla de Oro, XXII Olimpiada Nacional de Matemática Nivel Mayor (2010) "What we learned as children, that one plus one equals two, we know to be false. One plus one equals one. We even have a word when you plus another, equals one. That word is love." "Todos piensan en cambiar el mundo, pero nadie piensa en cambiarse a sí mismo."

Gerardo Soto Ver Perfil del Miembro Ver los mensajes de este miembro	May 21 2011, 02:56 PM Publicado: #26
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.648 Registrado: 16-April 10 Desde: Dalcahue-Chiloe Miembro Nº: 68.853 Nacionalidad: Colegio/Liceo: Sexo:	Gracias por el material. -------------------- >>He robado princesas a reyes agónicos. Incendié la ciudad de Trebon. He pasado la noche con Felurian y he despertado vivo y cuerdo. Me expulsaron de la Universidad a una edad a la que a la mayoría todavía no los dejan entrar. He recorrido de noche caminos de los que otros no se atreven a hablar ni siquiera de día. He hablado con Dioses, he amado a mujeres y he escrito canciones que hacen llorar a los bardos.<< <<Me llamo Kvothe (<Cuouz>). Quizá hayas oído hablar de mí.”>> El nombre del viento, primer dìa de la historia de Kvothe .-“Todo hombre sabio le teme a tres cosas: Una noche sin luna, una tormenta en el mar y a la ira de un hombre bueno.”” Citas del Nombre del viento .-Me llamo kvothe, que se pronuncia <<cuouz>>. Los nombres son importantes porque dicen mucho sobre las personas. He tenido más nombres de los que nadie merece.Los Adem me llaman Maedre. Que, según como se pronuncie, puede significar la Llama, el Trueno o el Árbol Partido. Mi primer mentor me llamaba E'lir porque yo era listo y lo sabìa. Mi primera amante me llamaba Dulator porque le gustaba cómo sonaba. Me han llamado Kvothe el Sin Sangre, Kvothe el Arcano y Kvothe el Asesino de Reyes. Todos esos nombres me los he ganado. Pero crecí siendo Kvothe. Una vez mi padre me dijo que significaba <<saber>>. .-“Y soy Edena Ruh hasta la médula. Lo que significa que mi sangre es roja. Significa que respiro aire puro y camino por donde me llevan los pies. No me arrastro ni me acobardo como un perro ante nadie por el hecho de que tenga un título. Eso lo interpretan como orgullo quienes se han pasado la vida lamiéndoles el culo a los demás.”(Kvothe) .-“Te lo juro por toda la sal que hay en mí: si contravienes mis deseos, el resto de tu breve existencia será una orquesta de desgracias. Lo juro por la piedra, el roble y el olmo: te convertiré en mi blanco. Te seguiré sin que me veas y apagaré cualquier chispa de placer que encuentres. Jamás conocerás la caricia de una mujer, un momento de descanso, un instante de paz. Y juro por el cielo nocturno y por la luna que si perjudicas a mi maestro, te abriré en canal y saltaré en tus entrañas como un niño en un charco. Encordaré un violín con tus tripas y te haré tocarlo mientras bailo.” .-Puedes dividir infinito un infinito número de veces, y el resultado seguirá siendo más infinito”, dijo Uresh con su extraño acento Lenatti. “Pero si divides un número no infinito un número infinito de veces el resultado no es menos infinito. Puesto que es menos infinito, pero hay un número infinito de ellos, si los sumas de nuevo, su suma da infinito. Eso implica que todo número es, de hecho, infinito. .-‎ Tengo tendencia a pensar demasiado, Bast. Mis mayores éxitos fueron producto de decisiones que tomé cuando dejé de pensar e hice sencillamente lo que me parecía correcto. Aunque no hubiera ninguna buena explicación para lo que había hecho. Aunque hubiera muy buenas razones para que no hiciese lo que hice.(Kvothe) .-Sí, soy un mito. Un mito muy especial que se crea a sí mismo. Las mejores mentiras sobre mí son las que yo mismo he contado.´ (Kvothe) .-Solo los locos y los sacerdotes no le temen a nada, y yo no me llevo muy bien con Dios (Kvothe) .-La musica es una amante celosa y temperamental, si le dedicas tiempo sera tuya pero si la desairas se ira y cuando la busques no la hallaras…(Kvothe) .-Las palabras sonpálidas sombras de nombres olvidados. Los nombres tienen poder, y las palabras también. Las palabras pueden hacer prender el fuego en la mente de los hombres. Las palabras pueden arrancarles lágrimas a los corazones más duros. Existen siete palabras que harán que una persona te ame. Existen diez palabras que minarán la más poderosa voluntad de un hombre. Pero una palabra no es más que la representación de un fuego. Un nombre es el fuego en sí. -Elodin .-Cronista pensó, sin proponérselo, en una historia que había oído. Una de tantas. Era el relato de cómo Kvothe había perseguido el deseo de su corazón. Tuvo que engañar a un demonio para conseguirlo. Pero una vez conseguido, tuvo que pelear con un ángel para conservarlo. «Es cierto —pensó Cronista—. Antes solo era una historia, pero ahora puedo creer en ella. Esta es la cara de un hombre que ha matado a un ángel. .-“Yo hasta que no vea una pantorrilla femenina al aire, no daré por inaugurada la primavera”(Bast) .- “Al pan, pan y al vino, vino. Pero a una prostituta llámala siempre señora. Tienen una vida muy dura y no cuesta nada ser amables con ellas.” .-Observando las caras que me rodeaban vi a una joven de no más de veinte años. Tenía un rostro dulce y los ojos azul claro. Sus labios parecían hechos para besar. Di un paso hacia ella, decidido a cogerla en brazos y… Me paré en seco cuando empezaba a estirar un brazo para acariciarle el cuello, y sentí algo muy parecido al vértigo. Allí las cosas eran diferentes. Era evidente que el hombre que estaba sentado al lado de la joven era su marido. Eso era importante, ¿no? Parecía un hecho muy impreciso y distante. ¿Por qué no iba desnudo, no comía violetas ni tocaba el laúd a cielo abierto? Volví a pasear la mirada por la taberna y todo aquello me pareció sumamente ridículo. Aquella gente sentada en los bancos, con capas y más capas de ropa, comiendo con cuchillo y tenedor. Lo encontraba todo absurdo y artificioso. Era increíblemente gracioso. Parecía que estuvieran jugando a un juego y ni siquiera se dieran cuenta. Era como un chiste que hasta entonces no había entendido. Me reí. (ETDUHS) .-- No has traido tu laud – me comentó cuando hubimos terminado de comer. -Esta noche tengo que irme a leer-dije-. Para entonces ya habría hecho el examen de admisión, y no haría falta que siguiera estudiando. Auri arrugó su carita. -Cinco dias no es pronto -dijo-. Pronto es mañana. -Cinco días es pronto para una piedra-argumenté. -Pues entonces toca para una piedra dentro de cinco días-replicó ella-. Y toca para mí mañana.(Auri) .-“Verá, maestro Kilvin: según los alumnos, lo rompí de un solo puñetazo de mi todopoderosa mano” .-“No has oído ni la primera nota de la música que me impulsa” .-“Viajé, amé, perdí, confié y me traicionaron.” .-“No me cansaba de mirar a Denna. Estaba sentada a mi lado, abrazándose las rodillas. Su piel era más luminosa que la luna, y sus ojos, más enormes que el cielo, más profundos que el agua, más oscuros que la noche” .-Sobré él verteré el hambre y el fuego hasta que la desolación lo aturda y todos los demonios de la oscuridad exterior miren asombrados y reconozcan que la especialidad del hombre es la venganza. .-“Aunque este empapado de ti, ardo. El movimiento de tu cabeza al volverse es como una canción. Es como una chispa. Es como un aliento que me infla y sopla para avivar un fuego que extenderse y rugir tu nombre no pueda evitar” .-“He oído lo que los poetas escriben sobre las mujeres. Componen rimas y rapsodias, y mienten. He visto a marineros en la orilla contemplando en silencio la lenta ondulación del mar. He visto a viejos soldados con el corazón de cuero que derramaban lágrimas al ver los colores de su rey ondeando al viento. Creedme: esos hombres no saben nada del amor. Amamos lo que amamos. La razón no entra en juego. En muchos aspectos, el amor más insensato es el amor más verdadero. Cualquiera puede amar algo por algún motivo. Eso es tan fácil como meterse un penique en el bolsillo. Pero amar algo a pesar de algo es otra cosa. Conocer los defectos y amarlos también. Eso es inusual, puro y perfecto.” Kvothe .-“La experiencia me ha enseñado que la mejor forma de protegerte es hacer creer a tus enemigos que no pueden hacerte daño” Para saber más de la trilogía de Patrick Rothfuss Click aquí

« Posterior · Material de Entrenamiento · Anterior »

3 Páginas:

< 1 2 3

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 30th April 2025 - 10:20 AM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.