|
|
|
|
|
|
|
  |
 Oct 21 2010, 05:31 PM Oct 21 2010, 05:31 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 1.559 Registrado: 18-November 07 Miembro Nº: 12.754 Nacionalidad:  Sexo:  |
22ª OLIMPIADA NACIONAL DE MATEMÁTICAS Prueba Final, Nivel Mayor Primera Prueba Problema 1:Los números enteros 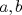 satisfacen la siguiente identidad: satisfacen la siguiente identidad: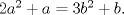 Pruebe que 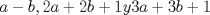 son cuadrados perfectos. son cuadrados perfectos.Problema 2: Determine cuál de los siguientes números es mayor, 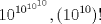 Problema 3: Los lados BC, CA, y AB de un triángulo ABC son tangentes a una circunferencia en los puntos X,Y,Z respectivamente. Demuestre que el centro de tal circunferencia está sobre la recta que pasa por los puntos medios de BC y AX. Primera Prueba[/b] Problema 4:Sean 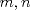 números enteros tales que satisfacen que números enteros tales que satisfacen que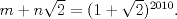 Encuentre el resto que se obtiene al dividir  por 5. por 5.Problema 5: Considere una recta 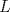 en el plano y sean en el plano y sean  puntos distintos en puntos distintos en 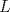 . Sea . Sea 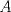 un punto que no está en un punto que no está en 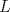 . Muestre que existe . Muestre que existe 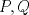 en en 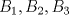 con con 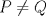 de tal modo que la distancia de de tal modo que la distancia de 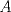 a a 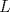 es mayor que la distancia de es mayor que la distancia de 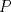 a la recta que pasa por a la recta que pasa por 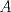 y y 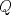 . .Problema 6: Pruebe que en el interior de un triángulo equilátero de lado  se puede poner una cantidad finita de círculos iguales que no se traslapen, de radio se puede poner una cantidad finita de círculos iguales que no se traslapen, de radio 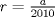 , de manera que la suma de sus áreas sea mayor que , de manera que la suma de sus áreas sea mayor que 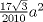 . .Mensaje modificado por Hamon el Oct 22 2010, 08:55 PM -------------------- Empezando con Desigualdades? Encuentra aquí problemas resueltos
|
|
|
|
 Oct 21 2010, 05:48 PM Oct 21 2010, 05:48 PM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 1.559 Registrado: 18-November 07 Miembro Nº: 12.754 Nacionalidad:  Sexo:  |
Hola, ojalá opinen de la prueba aquí mismo. La subo para comentarla, resolverla y obviamente para tenerla en nuestro querido FMAT.
Personalmente, la encontré bastante complicada. Quizás no tanto por los problemas, sino que me cabecié bastante con el 1 y el 3. Para el 2, por suerte, se me ocurrió una buena idea. El 1, lo dejé a medias, no se me ocurrió más, y el 3...me mató Bueno, basta de palabrerías, tiraré la idea de mi solución para el problema 2: Probaremos por inducción, que para n natural, mayor o igual que 2, se cumple lo siguiente: 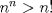 Para 2, nuestra proposición es cierta: 4 es mayor que 2. Luego, por proceso inductivo, asumamos que para un cierto n, la proposición es cierta. Demostraremos entonces que se cumplirá también para el sucesor de n; n+1. 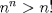 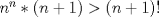 Además; 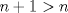 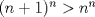 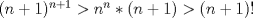 QED QEDLuego, por el proceso inductvo, hemos demostrado que la primera expresión es mayor que la segunda, para todo n natural, mayor que 1. Nota: Todas las multiplicaciones, y potencias efectuadas en las desigualdades, estan bien definidas, pues n es positivo. Saludos! Posteense un hint pa los que no hicimos el 3 U.U Mensaje modificado por Hamon el Oct 21 2010, 05:51 PM -------------------- Empezando con Desigualdades? Encuentra aquí problemas resueltos
|
|
|
|
 Oct 21 2010, 06:27 PM Oct 21 2010, 06:27 PM
Publicado:
#3
|
|
|
Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 15 Registrado: 8-May 09 Miembro Nº: 50.689 Nacionalidad:  Colegio/Liceo:  Sexo:  |
**** tocayo, igual que a ti. Creo que el 2 lo hize mas simple, separando el factorial y despues estableciendo desigualdades. Pero el P1 y P3 u.u me dio mucha lata el p3, porque habia estudiao geometria, de hecho justo habia estudiao ceva, menelao y esas cosas pero aqui no caxe nunca como aplicarlo, despues me comentaron como se hacia :/ Sera, mañana nose, ojala que se pueda hacer algo xd
|
|
|
|
 Oct 21 2010, 06:32 PM Oct 21 2010, 06:32 PM
Publicado:
#4
|
|
|
Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 15 Registrado: 8-May 09 Miembro Nº: 50.689 Nacionalidad:  Colegio/Liceo:  Sexo:  |
A, bueno, pal p3 segun me comentaron, podias tirar bisetrices para usar el teo de la bisectriz y dejar los trazos (que luegos ocuparias con Menelao) en funcion de los lados. De ahi Menelao y parece que estaba
|
|
|
|
 Oct 21 2010, 06:37 PM Oct 21 2010, 06:37 PM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 1.559 Registrado: 18-November 07 Miembro Nº: 12.754 Nacionalidad:  Sexo:  |
A, bueno, pal p3 segun me comentaron, podias tirar bisetrices para usar el teo de la bisectriz y dejar los trazos (que luegos ocuparias con Menelao) en funcion de los lados. De ahi Menelao y parece que estaba que rabia!!! me sonaba el probelma, no se me ocurrio usar menelao eso que me lo sé y habia "repasado" la formula!! debe ser bonita oslucion, ahora la buscaré. gracias por responder, a estar más lucidos mañana!! -------------------- Empezando con Desigualdades? Encuentra aquí problemas resueltos
|
|
|
|
 Oct 21 2010, 07:40 PM Oct 21 2010, 07:40 PM
Publicado:
#6
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 532 Registrado: 19-October 08 Desde: Santa Cruz de la Sierra Miembro Nº: 36.531 Nacionalidad:  Sexo:  |
Creo que me salio muy lindo con homotecia.
 Sea  el punto medio de el punto medio de 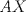 Sea Sea 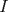 el incentro de el incentro de 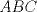 . Sea . Sea 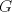 el punto diametralmente opuesto a el punto diametralmente opuesto a 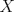 con respecto al incirculo de con respecto al incirculo de 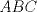 . Sea . Sea 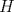 el punto de tangencia del excirculo de el punto de tangencia del excirculo de 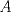 (respecto a (respecto a 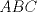 ) con ) con 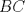 . Sean . Sean 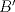 y y 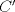 la interseccion de la interseccion de 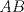 y y 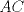 con la paralela a con la paralela a 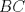 por por 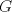 , respectivamente. Los triangulos , respectivamente. Los triangulos 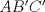 y y 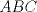 son homoteticos con centro en son homoteticos con centro en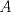 . El incirculo de . El incirculo de 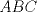 es el excirculo de es el excirculo de 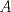 con respecto a con respecto a 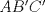 de donde los puntos de donde los puntos 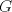 y y 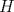 son homologos, y por lo tanto, colineales con son homologos, y por lo tanto, colineales con 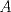 . Es facil ver que . Es facil ver que 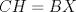 haciendo calculos sencillos. Tenemos que haciendo calculos sencillos. Tenemos que 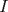 es el punto medio de es el punto medio de 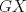 de donde de donde 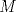 es el punto medio de es el punto medio de 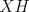 . Pero . Pero 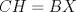 de donde de donde 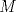 es el punto medio de es el punto medio de 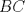 demostrando lo pedido demostrando lo pedido
-------------------- "I've never let my school interfere with my education.”
|
|
|
|
 Oct 21 2010, 07:52 PM Oct 21 2010, 07:52 PM
Publicado:
#7
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 836 Registrado: 9-January 07 Desde: Santiasko Miembro Nº: 3.659 Nacionalidad:  Sexo:  |
|
|
|
|
 Oct 21 2010, 08:01 PM Oct 21 2010, 08:01 PM
Publicado:
#8
|
|
 Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 1.559 Registrado: 18-November 07 Miembro Nº: 12.754 Nacionalidad:  Sexo:  |
gracias por el aporte...igual esta volao el documento ap mi gusto xD...me da lata, que en la nacional pongan problemas que sean "conocidos" (relativamente), pues para los exprimentados es como repetir la solucion, y para los nuevos es injusto pues hay gente que ya los ha visto xD. Bueno, será pos, a leer el pdf gracias por compartirlo -------------------- Empezando con Desigualdades? Encuentra aquí problemas resueltos
|
|
|
|
 Oct 21 2010, 08:02 PM Oct 21 2010, 08:02 PM
Publicado:
#9
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 79 Registrado: 27-April 10 Desde: Talagante Miembro Nº: 69.788 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
tambien me mató el P3
Mensaje modificado por josezero07 el Oct 21 2010, 08:03 PM --------------------    |
|
|
|
 Oct 21 2010, 08:08 PM Oct 21 2010, 08:08 PM
Publicado:
#10
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 858 Registrado: 20-August 09 Desde: In my House Miembro Nº: 57.323 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Primer problema de geometría decente que veo en la nacional
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 30th April 2025 - 07:03 PM |












