|
|
|
|
|
|
|
  |
 Oct 22 2010, 12:36 PM Oct 22 2010, 12:36 PM
Publicado:
#21
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 532 Registrado: 19-October 08 Desde: Santa Cruz de la Sierra Miembro Nº: 36.531 Nacionalidad:  Sexo:  |
No se si estaré muleando, pero ese ejercicio me parece como obvio mira: 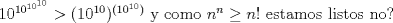 pienso exactamente lo mismo. -------------------- "I've never let my school interfere with my education.”
|
|
|
|
 Oct 22 2010, 07:13 PM Oct 22 2010, 07:13 PM
Publicado:
#22
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Bueno, tengo entendido que
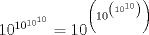 . Aún así, no debería ser difícil. . Aún así, no debería ser difícil.Estamos a la espera de la segunda parte y, por supuesto, de la prueba nivel menor. Saludos -------------------- |
|
|
|
 Oct 22 2010, 08:39 PM Oct 22 2010, 08:39 PM
Publicado:
#23
|
|
 Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 1.559 Registrado: 18-November 07 Miembro Nº: 12.754 Nacionalidad:  Sexo:  |
Bueno, tengo entendido que 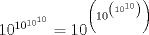 . Aún así, no debería ser difícil. . Aún así, no debería ser difícil.Estamos a la espera de la segunda parte y, por supuesto, de la prueba nivel menor. Saludos a sus órdenes!! -------------------- Empezando con Desigualdades? Encuentra aquí problemas resueltos
|
|
|
|
 Oct 23 2010, 10:27 AM Oct 23 2010, 10:27 AM
Publicado:
#24
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.139 Registrado: 11-June 08 Desde: UK Miembro Nº: 26.837 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
p4)
Fácilmente vemos que si 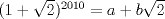 entonces entonces 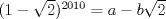 , es decir, el coeficiente , es decir, el coeficiente  lo podemos calcular fácilmente evaluando la diferencia de los términos anteriores. lo podemos calcular fácilmente evaluando la diferencia de los términos anteriores.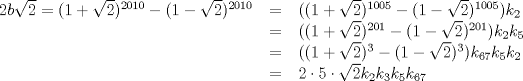 Donde 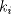 es el otro miembro de la factorización, por ejemplo es el otro miembro de la factorización, por ejemplo 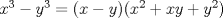 entonces entonces  tomando en este caso tomando en este caso 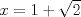 e e 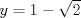 . De esto se concluye que . De esto se concluye que 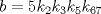 entonces el resto es 0 entonces el resto es 0
-------------------- blep
|
|
|
|
 Oct 23 2010, 04:18 PM Oct 23 2010, 04:18 PM
Publicado:
#25
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 532 Registrado: 19-October 08 Desde: Santa Cruz de la Sierra Miembro Nº: 36.531 Nacionalidad:  Sexo:  |
No se si habre entendido mal pero el 5 parece trivial.
Sea 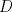 el pie de la altura de el pie de la altura de 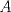 sobre sobre 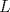 . Por principio de palomares, existen . Por principio de palomares, existen 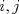 tales que tales que 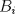 y y 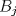 estan en el mismo lado de estan en el mismo lado de 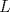 respecto a respecto a 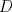 . Podemos suponer que . Podemos suponer que 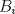 esta entre esta entre 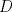 y y 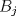 . Tomamos . Tomamos  y y 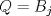 . Es facil ver que verifica la condicion . Es facil ver que verifica la condicion
Mensaje modificado por xD13G0x el Oct 23 2010, 04:19 PM -------------------- "I've never let my school interfere with my education.”
|
|
|
|
 Oct 23 2010, 06:24 PM Oct 23 2010, 06:24 PM
Publicado:
#26
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 234 Registrado: 5-April 10 Desde: Arg Miembro Nº: 67.793 Nacionalidad:  Sexo:  |
Hola, ojalá opinen de la prueba aquí mismo. La subo para comentarla, resolverla y obviamente para tenerla en nuestro querido FMAT. Personalmente, la encontré bastante complicada. Quizás no tanto por los problemas, sino que me cabecié bastante con el 1 y el 3. Para el 2, por suerte, se me ocurrió una buena idea. El 1, lo dejé a medias, no se me ocurrió más, y el 3...me mató Bueno, basta de palabrerías, tiraré la idea de mi solución para el problema 2: Probaremos por inducción, que para n natural, mayor o igual que 2, se cumple lo siguiente: 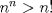 Para 2, nuestra proposición es cierta: 4 es mayor que 2. Luego, por proceso inductivo, asumamos que para un cierto n, la proposición es cierta. Demostraremos entonces que se cumplirá también para el sucesor de n; n+1. 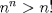 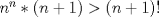 Además; 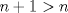 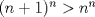 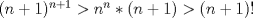 QED QEDLuego, por el proceso inductvo, hemos demostrado que la primera expresión es mayor que la segunda, para todo n natural, mayor que 1. Nota: Todas las multiplicaciones, y potencias efectuadas en las desigualdades, estan bien definidas, pues n es positivo. Saludos! Posteense un hint pa los que no hicimos el 3 U.U Hay un problema en tu solucion, le falta un pequenio caso, el problema pide ver si 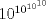 es mayor que es mayor que 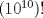 vos lo q demostraste es que vos lo q demostraste es que 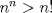 para para 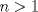 , pero si tomamos , pero si tomamos 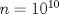 : : 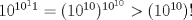 , te falto aclarar que , te falto aclarar que 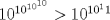 lo que es trivial lo que es trivial -------------------- 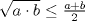 |
|
|
|
 Oct 23 2010, 07:55 PM Oct 23 2010, 07:55 PM
Publicado:
#27
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.169 Registrado: 11-June 08 Desde: rancagua Miembro Nº: 26.922 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
yo kiero sacarme la duda si lo que hice esta bien
sí, ya terminó pero igual ![TEX: \[<br />a = 10^{10} \Rightarrow 10^{10^{10^{10} } } = 10^{10^a } \wedge 10^{10} ! = a!<br />\]<br />](./tex/ad79c8377390e957542c4ea8bf9b354f.png) sea las funciones ![TEX: \[<br />\begin{gathered}<br /> f(a) = 10^{10^a } \hfill \\<br /> g(a) = a! \hfill \\ <br />\end{gathered} <br />\]<br />](./tex/033822f1f74385e621946e760760ccd1.png) ![TEX: \[<br />\frac{{g(a)}}<br />{{f(a)}}<br />\]<br />](./tex/250b7e1bf295083f908d6de4e55e66f3.png) de modo que si de modo que si ![TEX: \[<br />f(a) > g(a)<br />\]<br />](./tex/28cf7363045fec83ff71a356b73ec623.png) converge a 0 converge a 0probemos si converge entonces: ![TEX: \[<br />\mathop {\lim }\limits_{a \to \infty } \frac{{a!}}<br />{{10^{10^a } }}<br />\]<br />](./tex/27db58a67039b07eb2e3422aa37ff744.png) si derivamos 'a' veces entonces notamos que el numerador converge a 1 mientras que el denominador sigue creciendo de manera que ![TEX: \[<br />f(a) > g(a)<br />\]<br />](./tex/c309a2f86e794c3e1b8773e401f257a2.png) demostrando asi que ![TEX: \[<br />10^{10^{10^{10} } } > 10^{10} !<br />\]<br />](./tex/dea45646a44f12d8ceebb7daa9cdbc8b.png)
Mensaje modificado por fabiannx15 el Oct 23 2010, 07:57 PM -------------------- Richard Fabian Jerez
Ex alumno del Liceo Oscar Castro 4ºL matemático ¿Necesitas ayuda para la psu y no tienes dinero?: Agrega a logratus850@hotmail.com y comienza a preguntar! Somos un grupo de universitarios dispuestos a ayudarte de manera gratuita para que logres tus sueños, todos tuvimos como promedio más de 800 puntos en la PSU. Team PSU 2010!! Únete!  [color="#000080"][/color] [color="#000080"][/color] |
|
|
|
 Oct 23 2010, 08:31 PM Oct 23 2010, 08:31 PM
Publicado:
#28
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.139 Registrado: 11-June 08 Desde: UK Miembro Nº: 26.837 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
yo kiero sacarme la duda si lo que hice esta bien sí, ya terminó pero igual ![TEX: \[<br />a = 10^{10} \Rightarrow 10^{10^{10^{10} } } = 10^{10^a } \wedge 10^{10} ! = a!<br />\]<br />](./tex/ad79c8377390e957542c4ea8bf9b354f.png) sea las funciones ![TEX: \[<br />\begin{gathered}<br /> f(a) = 10^{10^a } \hfill \\<br /> g(a) = a! \hfill \\ <br />\end{gathered} <br />\]<br />](./tex/033822f1f74385e621946e760760ccd1.png) ![TEX: \[<br />\frac{{g(a)}}<br />{{f(a)}}<br />\]<br />](./tex/250b7e1bf295083f908d6de4e55e66f3.png) de modo que si de modo que si ![TEX: \[<br />f(a) > g(a)<br />\]<br />](./tex/28cf7363045fec83ff71a356b73ec623.png) converge a 0 converge a 0probemos si converge entonces: ![TEX: \[<br />\mathop {\lim }\limits_{a \to \infty } \frac{{a!}}<br />{{10^{10^a } }}<br />\]<br />](./tex/27db58a67039b07eb2e3422aa37ff744.png) si derivamos 'a' veces entonces notamos que el numerador converge a 1 mientras que el denominador sigue creciendo de manera que ![TEX: \[<br />f(a) > g(a)<br />\]<br />](./tex/c309a2f86e794c3e1b8773e401f257a2.png) demostrando asi que ![TEX: \[<br />10^{10^{10^{10} } } > 10^{10} !<br />\]<br />](./tex/dea45646a44f12d8ceebb7daa9cdbc8b.png) El problema es que l'hôpital se define para limite de funciones, aca estas derivando un factorial... como definirias por ejemplo 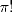 -------------------- blep
|
|
|
|
 Oct 23 2010, 10:27 PM Oct 23 2010, 10:27 PM
Publicado:
#29
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 6 Registrado: 25-June 10 Miembro Nº: 73.207 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
P1.- 2a2+a=3b2+b
sabemos que a>b o a=b=0 en el caso que a>b a(2a+1)=b(3b+1) como a y 2a+1 son coprimos podemos decir que b divide a pero no 2a+1 o alreves entonces 2a2+a=3b2+b 2a2-2b2+a-b=b2 2(a+b)(a-b)+(a-b)=b2 (a-b)(2a+2b+1)=b2 como a y 2a+1 son coprimos, a-b y 2a+2b+1 son coprimos y su producto es un cuadrado entonces ambos son cuadrados perfectos. 2a2+a=3b2+b 3a2-3b2+a-b=a2 3(a+b)(a-b)+(a-b)=a2 (a-b)(1+3a+3b)=a2 a-b y 1+3a+3b tambien son coprimos y como su producto es un cuadrado perfecto entonces ambos son cuadrados perfectos. en el caso que a=b=0 la terna 0,1,1 son cuadrados perfectos entonces a-b,1+2a+2b,1+3a+3b son cuadrados perfectos |
|
|
|
 Oct 24 2010, 03:33 PM Oct 24 2010, 03:33 PM
Publicado:
#30
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.169 Registrado: 11-June 08 Desde: rancagua Miembro Nº: 26.922 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
El problema es que l'hôpital se define para limite de funciones, aca estas derivando un factorial... como definirias por ejemplo 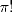 eske bueno aplicando definicion de factoriales tendriamos ![TEX: \[<br />a\left( {a - 1} \right)\left( {a - 2} \right)*...*3*2*1<br />\]<br />](./tex/20653547ba74590f97bed97da9b93a44.png) notamos que al derivar 'a' veces esto es 1 -------------------- Richard Fabian Jerez
Ex alumno del Liceo Oscar Castro 4ºL matemático ¿Necesitas ayuda para la psu y no tienes dinero?: Agrega a logratus850@hotmail.com y comienza a preguntar! Somos un grupo de universitarios dispuestos a ayudarte de manera gratuita para que logres tus sueños, todos tuvimos como promedio más de 800 puntos en la PSU. Team PSU 2010!! Únete!  [color="#000080"][/color] [color="#000080"][/color] |
|
|
|
  |
2 usuario(s) está(n) leyendo esta discusión (2 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 30th April 2025 - 01:10 PM |











