|
|
|
|
|
|
|
  |
 Jan 5 2011, 04:20 PM Jan 5 2011, 04:20 PM
Publicado:
#1
|
|
 Coordinador General Gran Maraton PSU Final 2008 Grupo: Moderador Mensajes: 1.607 Registrado: 11-June 07 Desde: Peñalolen, Stgo Miembro Nº: 6.641 Nacionalidad:  Universidad:  Sexo:  |
![TEX: \noindent \\<br />\begin{center}MAT2515 - Análisis Real\\<br />Interrogación II \end{center}<br />\begin{enumerate}<br />\item Sean $(X,\rho)$ y $(Y,\sigma)$ espacios metricos. En $Z = X \times Y$ se define la métrica $\tau((x,y),(\bar x,\bar y))= {\text{max}}(\rho(x,\bar x),\sigma(y,\bar y))$<br />\begin{enumerate}<br /> \item Demostrar que si $(X,\rho)$ y $(Y,\sigma)$ son completos entonces $(Z,\tau)$ es completo.<br /> \item Demostrar que si $(X,\rho)$ y $(Y,\sigma)$ son compactos entonces $(Z,\tau)$ es compacto.<br />\end{enumerate}<br /><br />\item Sea $X = \left\{ {f \in C[0,1]:|f(x)| \leqslant 1} \right\}$ y $\rho(f,g)={\text{ma}}{{\text{x}}_{x \in [0,1]}}|f(x) - g(x)| $.<br /><br />\begin{enumerate}<br /> \item Demostrar que $(X,\rho)$ es completo.<br /> \item Demostrar que existe una función $f:[0,1] \to \mathbb{R}$ tal que <br />$$f(x) = \int_0^x {\int_0^y {f(t){\text{sen}}(y)dtdy + \frac{1}<br />{2}\cos (x)} } $$<br /><br />más aún $f$ es continua y $|f(x)|\leqslant 1$ para todo $x$ en $[0,1]$.<br /> <br />\end{enumerate}<br /><br />\item Sea $f:[0,\infty) \to \mathbb{R}$ continua tal que ${\text{li}}{{\text{m}}_{x \to \infty }}f(x) = A$. Demostrar que $f$ es uniformemente continua en $[0,\infty)$.<br /><br />\item \begin{enumerate} \item Dar un ejemplo de un espacio métrico que no sea totalmente acotado.<br /> \item Demostrar que si $F:X \to Y$ es uniformemente continua y X es totalmente acotado entonces $F(X)$ también es totalmente acotado. <br />\end{enumerate}<br /><br />\end{enumerate}<br />](./tex/da9dd9362fee6f1ce580becea53df6b6.png) --------------------  |
|
|
|
 Jan 26 2012, 03:48 PM Jan 26 2012, 03:48 PM
Publicado:
#2
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 465 Registrado: 15-July 11 Miembro Nº: 91.905 Nacionalidad:  Universidad:  Sexo:  |
Problema 1:
1.a) Sea 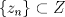 una sucesión de Cauchy en una sucesión de Cauchy en 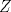 . Dado . Dado 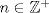 , escribamos , escribamos 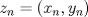 . Como . Como 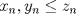 , se cumple que , se cumple que 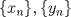 son sucesiones de Cauchy en son sucesiones de Cauchy en 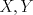 , respectivamente. Como , respectivamente. Como 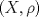 e e 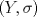 son completos, son completos, 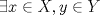 tales que tales que  e e 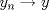 cuando cuando 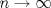 . Sea . Sea 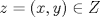 . Demostraremos que . Demostraremos que  cuando cuando 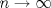 . . Dado 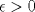 , sean , sean 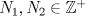 tales que si tales que si 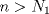 entonces entonces 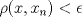 y si y si 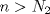 entonces entonces 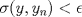 . Si . Si 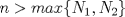 entonces entonces 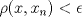 y y 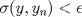 . Luego . Luego 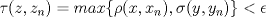 . Por lo tanto . Por lo tanto  . Como cada sucesión de Cauchy en . Como cada sucesión de Cauchy en 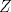 converge a un punto es converge a un punto es 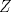 se concluye que se concluye que 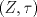 es completo. es completo.  1.b) Sea 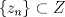 una sucesión. Dado una sucesión. Dado 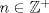 , escribamos , escribamos 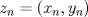 . Como . Como 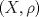 es compacto, la sucesión es compacto, la sucesión 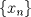 posee una subsucesión posee una subsucesión 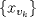 convergente a convergente a 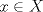 . Definamos . Definamos 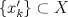 tal que tal que 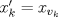 . Del mismo modo, sea . Del mismo modo, sea 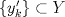 tal que tal que 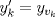 . Como . Como 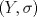 es compacto, es compacto, 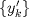 posee una subsucesión posee una subsucesión 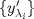 convergente a convergente a 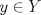 . Como . Como 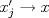 cuando cuando 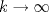 , se sigue que , se sigue que 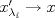 cuando cuando 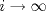 . Luego, . Luego, 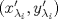 es una subsucesión de es una subsucesión de 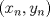 que converge a que converge a 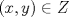 . Por lo tanto . Por lo tanto 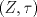 es compacto. es compacto. 
-------------------- He-llo? Could you say that again? More slowly? In a language I understand? Depending on what you said, I might kick your ass! |
|
|
|
 Jan 26 2012, 06:17 PM Jan 26 2012, 06:17 PM
Publicado:
#3
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 465 Registrado: 15-July 11 Miembro Nº: 91.905 Nacionalidad:  Universidad:  Sexo:  |
Problema 4:
4.a) Sea 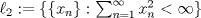 y y 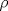 la métrica inducida por la norma la métrica inducida por la norma 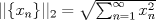 . Sea . Sea 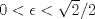 , y consideremos una sucesión , y consideremos una sucesión 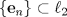 de modo que si de modo que si 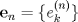 , entonces , entonces 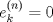 si si 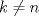 y y 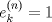 si si  . Vea que si . Vea que si 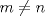 , entonces , entonces 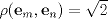 . Luego, . Luego, 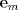 y y 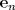 pertenecen a bolas de radio pertenecen a bolas de radio  disjuntas independiente de los centros que se ocupen. Por ende, no es posible cubrir disjuntas independiente de los centros que se ocupen. Por ende, no es posible cubrir 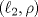 con una cantidad finita de bolas de radio con una cantidad finita de bolas de radio  , es decir, , es decir, 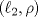 no es totalmente acotado. no es totalmente acotado.  4.b) Sea 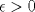 . Como . Como 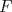 es uniformemente continua, es uniformemente continua, 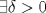 tal que tal que 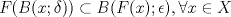 Como Como 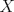 es totalmente acotado, es totalmente acotado, 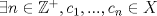 tales que tales que 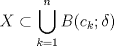 . Luego, se cumple que . Luego, se cumple que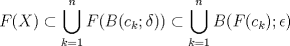 Por lo tanto 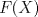 es totalmente acotado. es totalmente acotado.  2.a) Notar que ![TEX: $[-1,1]$](/tex-image/a95f0c5ceecf454f617b499c1c56d9f0.png) es cerrado en es cerrado en 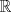 (el cual es completo), de donde (el cual es completo), de donde ![TEX: $[-1,1]$](/tex-image/4a74a38f4aeb6705470aa81f0c257c48.png) es completo. Usando el hecho que si es completo. Usando el hecho que si 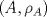 es un espacio métrico cualquiera y que es un espacio métrico cualquiera y que 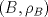 es un espacio métrico completo implica que es un espacio métrico completo implica que 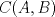 también sea completo, se concluye. también sea completo, se concluye.
Mensaje modificado por Cenizas con Mostaza el Jan 27 2012, 09:08 PM -------------------- He-llo? Could you say that again? More slowly? In a language I understand? Depending on what you said, I might kick your ass! |
|
|
|
 Mar 30 2013, 09:54 PM Mar 30 2013, 09:54 PM
Publicado:
#4
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 465 Registrado: 15-July 11 Miembro Nº: 91.905 Nacionalidad:  Universidad:  Sexo:  |
Preparando la I1 que se viene el miércoles...
2b) Defina 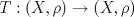 tal que si tal que si 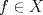 y y ![TEX: $x\in [0,1]$](/tex-image/31fadee9a85557f5ffa4422ce9a03cf4.png) , entonces , entonces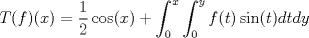 Se probará que efectivamente 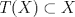 . Es sencillo ver que . Es sencillo ver que ![TEX: $T(f)\in C[0,1]$](/tex-image/d2c963e82a11a83b3987b0557d491738.png) y como y como ![TEX: $|f(x)|\leq 1,\forall x\in[0,1]$](/tex-image/500e4b5cf7610fa8cf2621fa1fce522f.png) , se cumple que , se cumple que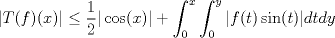 Como 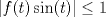 , entonces la integral se puede acotar por , entonces la integral se puede acotar por 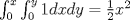 , luego , luego ![TEX: $|T(f)(x)|\leq \dfrac{1}{2}|\cos(x)|+\dfrac{1}{2}x^2\leq 1,\forall x\in [0,1]$](/tex-image/7243626c8980e85509b8b3d84e6682e5.png) Con esto se sigue que 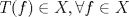 y se obtiene que y se obtiene que 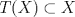 . A continuación, vea que si . A continuación, vea que si 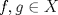 , entonces , entonces![TEX: $d(T(f),T(g))\leq \displaystyle \max_{x\in[0,1]} \displaystyle \int_0^x \int_0^y |\sin(t)||f(t)-g(t)|dtdy$](/tex-image/b48ccd283f9b7d40930fe406ff27d900.png) Como ![TEX: $(\forall t\in[0,1])((|f(t)-g(t)|\leq d(f,g))\wedge |\sin(t)|\leq 1)$](/tex-image/b36bed9ce1e021af5ca0f73663421b4c.png) , se sigue que , se sigue que![TEX: $d(T(f),T(g))\leq \displaystyle \max_{x\in[0,1]} \dfrac{1}{2}x^2d(f,g)=\dfrac{1}{2}d(f,g)$](/tex-image/daa700399e9378546449a004d73ef204.png) Esto significa que 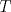 es una contracción de es una contracción de 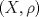 (el cual es completo por lo demostrado anteriormente) en sí mismo, y por el Teorema del Punto Fijo de Banach, se sigue (el cual es completo por lo demostrado anteriormente) en sí mismo, y por el Teorema del Punto Fijo de Banach, se sigue 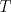 posee un único punto fijo. posee un único punto fijo. 
Mensaje modificado por Cenizas con Mostaza el Mar 30 2013, 09:56 PM -------------------- He-llo? Could you say that again? More slowly? In a language I understand? Depending on what you said, I might kick your ass! |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 29th October 2025 - 08:20 AM |







