 I1 Análisis Real, 2S 2011 |
|
|
|
|
|
|
Foro fmat.cl > Programa Enseñanza Universitaria > Comunidades Universitarias > Universidad Católica > Análisis Real  |
 Sep 9 2011, 09:54 PM
Publicado:
#1
|
|
 Staff Fmat  Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:   |
![TEX: \noindent \\<br />\begin{center}MAT2515 - Análisis Real\\<br />Interrogación I - Viernes 09 de Septiembre de 2011\end{center}<br />\begin{enumerate}<br />\item Sea $(X, \rho)$ un espacio métrico. Considere las siguientes afirmaciones. En caso de ser verdaderas demuéstrelas y en caso de ser falsas, dé un contraejemplo.<br />\begin{enumerate}<br />\item La unión finita de subconjuntos cerrados de $X$ es cerrada.<br />\item La unión arbitraria de subconjuntos cerrados de $X$ es cerrada.<br />\item La unión arbitraria de subconjuntos abiertos de $X$ es abierta.<br />\end{enumerate}<br />\item Sean $(X, \rho)$, $(Y, \sigma)$ espacios métricos y sea $f:X\rightarrow Y$ una función inyectiva tal que $f(E)$ es cerrado en $(Y, \sigma)$ para todo conjunto $E$ cerrado en $(X, \rho)$. Demuestre que $f^{-1}$ es continua en $f(X)$.<br />\item <br />\begin{enumerate}<br />\item Sea $(X, \rho)$ un espacio métrico y sea $A\subset X$ un conjunto finito. ¿Es $A$ conexo? Justifique su respuesta.<br />\item Considere $\mathbb{R}$ con la métrica usual. Demuestre que los intervalos son conexos.<br />\end{enumerate}<br />\item <br />\begin{enumerate}<br />\item Enuncie el Teorema del punto fijo de Banach.<br />\item Sean $a, b$ funciones reales continuas en el intervalo $[0,1]$. Usando el Teorema del punto fijo de Banach demuestre que existe $\delta >0$ de manera que el problema de valor inicial<br />\begin{center}<br />$y'(x) = a(x)y(x)+b(x), y(\frac{1}{2}) = 0\ (1)$<br />\end{center}<br />tiene una única solución definida en el intervalo $(\frac{1}{2}-\delta, \frac{1}{2}+\delta)$. (Se dice que $y$ es solución de este problema de valor inicial en $(\frac{1}{2}-\delta, \frac{1}{2}+\delta)$ si $y$ es diferenciable en $(\frac{1}{2}-\delta, \frac{1}{2}+\delta)$ y satisface $(1)$ en dicho intervalo).<br />\end{enumerate}<br />\end{enumerate}<br />](/tex-image/f8ac7bfb08982d404471cc4bc471fab7.png)
-------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
 |
 
|
|
Nov 24 2011, 01:30 AM
Publicado:
#2
|
|
 Dios Matemático Supremo  Grupo: Usuario FMAT Mensajes: 1.767 Registrado: 21-January 08 Desde: Santiago - Ancud Miembro Nº: 14.865 Nacionalidad: Colegio/Liceo:  Universidad:  Sexo: |
La 3a)
Si X tiene un elemento, es claro que es conexo. En el caso contrario: Si X es un espacio métrico finito, entonces el mínimo m de las distancias entre todos los pares de elementos es un número no nulo, de modo que si tomamos una bola de radio m/2 centrada en torno a cada punto del espacio, tenemos una separación del espacio en más que dos abiertos. Concluímos que X no es conexo. Otra forma: sea (X,d) es un espacio métrico finito con más de un elemento, z e y dos puntos X. Entonces si X fuera conexo, la función definida por f(x)=d(y,x) toma los valores 0 en x=y y un valor mayor que 0 en x=z, digamos que vale p. Luego, por TVI, como X es conexo, f toma todos los valores entre 0 y p, lo cual es imposible porque X es finito y f es función. En el fondo, con el segundo argumento uno demuestra algo más fuerte: Si X es un espacio métrico conexo con al menos dos elementos, entonces 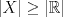 .Saludos, y a aportar más y dar menos jugo. -------------------- Estudia para superarte a ti mismo, no al resto. |
|
|
|
|
Nov 24 2011, 09:11 AM
Publicado:
#3
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad: Colegio/Liceo:  Sexo:  |
Solo voy a criticar constructivamente la prueba, no resolveré nada:
- Los primeros ejercicios son puros rudimentos, estoy de acuerdo con el comentario de jc_08. - A juzgar por el problema 4 diría que se nota demasiado que quien dicta el ramo trabaja en EDP, y eso igual es malo porque se supone que el objetivo del curso es que los estudiantes manejen correctamente las definiciones y propiedades de los conceptos de continuidad y derivados en contextos generales (no necesariamente espacios métricos); entonces como que se coarta un poco la visión ddel estudiante al decir "si, este teorema se usa en parciales..." siendo que tiene unas aplicaciones tránfugas bastante raras. PD: la prueba evalúa topología obviamente, porque es la I1.... -------------------- |
|
|
|
|
Nov 24 2011, 07:49 PM
Publicado:
#4
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.918 Registrado: 14-May 08 Desde: The Tower of God Miembro Nº: 23.100 Nacionalidad: Colegio/Liceo: Universidad: Sexo: |
El ramo lo da MGH, es obvio que la I va a ser muy parecida al Burkill pos, si prácticamente lee el libro en la clase.
Too caso eso no significa que el curso sea fácil, de hecho conozco gente muy seca haciendo el curso, y digamos que sus notas no son muy buenas. Una cosa es ver las pruebas de afuera que dentro de la sala, supongo que todos saben eso. Esop, sorry para los que no caxaban mucho de la cuestión en la cato. Saludos -------------------- |
|
|
|
|
Nov 24 2011, 08:04 PM
Publicado:
#5
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 125 Registrado: 14-March 09 Miembro Nº: 44.905 Nacionalidad: Sexo: |
CITA(Kaissa @ Nov 24 2011, 10:11 AM)  Solo voy a criticar constructivamente la prueba, no resolveré nada: - Los primeros ejercicios son puros rudimentos, estoy de acuerdo con el comentario de jc_08. - A juzgar por el problema 4 diría que se nota demasiado que quien dicta el ramo trabaja en EDP, y eso igual es malo porque se supone que el objetivo del curso es que los estudiantes manejen correctamente las definiciones y propiedades de los conceptos de continuidad y derivados en contextos generales (no necesariamente espacios métricos); entonces como que se coarta un poco la visión ddel estudiante al decir "si, este teorema se usa en parciales..." siendo que tiene unas aplicaciones tránfugas bastante raras. PD: la prueba evalúa topología obviamente, porque es la I1.... como que nadie sabe cual es mi comentario en fin  , ahora me censuraron y por primera vez dije algo en buena onda..... dije que era topologia y hasta recomende el burkill, como lo hizo KURA cual es mi pecado mortal?
--------------------    |
|
|
|
|
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 30th April 2025 - 09:50 AM |
