I1 s2 2011 - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa Enseñanza Universitaria > Comunidades Universitarias > Universidad Católica > Álgebra Abstracta

Reply to this topic

Start new topic

I1 s2 2011

felper Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 17 2011, 07:35 PM Publicado: #1
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.767 Registrado: 21-January 08 Desde: Santiago - Ancud Miembro Nº: 14.865 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	I1 s2 2011 Profesor: Rafael Tiedra Problema 1 Demostrar la siguiente proposición: 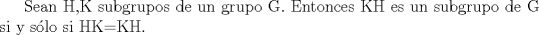$TEX: Sean $H$ ,$K$ subgrupos de un grupo $G$. Entonces $KH$ es un subgrupo de $G$ si y sólo si $HK=KH$.$ Problema 2 a) 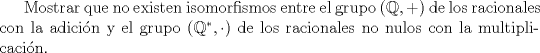$TEX: Mostrar que no existen isomorfismos entre el grupo $(\mathbb{Q},+)$ de los racionales con la adición y el grupo $(\mathbb{Q}^*,\cdot)$ de los racionales no nulos con la multiplicación.$ b) Demostrar la siguiente proposición de Cauchy 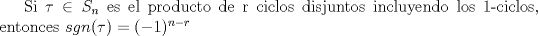$TEX: Si $\tau \in S_n$ es el producto de $r$ ciclos disjuntos incluyendo los 1-ciclos, entonces $sgn(\tau)=(-1)^{n-r}$$ Problema 3 $TEX: Sea $G$ un grupo y $\left[ G,G \right]$ el subgrupo de G generado por los elementos conmutadores $aba^{-1}b^{-1}$, es decir<br />$$ \left[ G,G\right] =< \{ aba^{-1}b^{-1} \| a,b\in G \}> $$<br />Mostrar que $\left[ G,G \right]$ es normal en $G$.$ Problema 4 a) 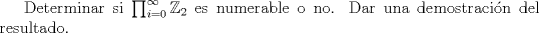$TEX: Determinar si $\prod_{i=0}^{\infty}\mathb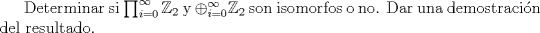b{Z}_2$ es numerable o no. Dar una demostración del resultado.$ b) $TEX: Determinar si $\prod_{i=0}^{\infty}\mathbb{Z}_2$ y $\oplus_{i=0}^{\infty}\mathbb{Z}_2$ son isomorfos o no. Dar una demostración del resultado.$ -------------------- Estudia para superarte a ti mismo, no al resto.

Gastón Burrull	Oct 17 2011, 09:36 PM Publicado: #2
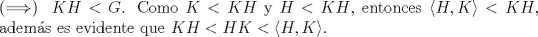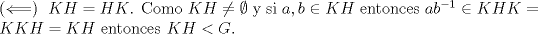
Invitado	P1) $TEX: \noindent ($\Longrightarrow$) $\ KH<G$. Como $K<KH$ y $H<KH$, entonces $\left<H,K\right><KH$, además es evidente que $KH<HK<\left<H,K\right>$.$ $TEX: \noindent ($\Longleftarrow$) $\ KH=HK$. Como $KH\neq \emptyset$ y si $a,b\in KH$ entonces $ab^{-1}\in KHK=KKH=KH$ entonces $KH<G$.$

Gastón Burrull	Oct 17 2011, 10:00 PM Publicado: #3
Invitado	P3) $TEX: \noindent $[G,G]=[G,G]^g$. Pues $(aba^{-1}b^{-1})^g=a^gb^g(a^g)^{-1}(b^g)^{-1}\in [G,G]$.$

Arkjham Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 17 2011, 10:15 PM Publicado: #4
Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 16 Registrado: 17-October 11 Miembro Nº: 95.840 Nacionalidad: Sexo:	$TEX: Digamos que <br />$$<br />\sigma = \prod\limits_{i = 1}^n {\alpha _i } <br />$$<br />es la descomposición en ciclos disjuntos de $$<br />\sigma <br />$$<br />si $ r_i $ es el largo del ciclo $$<br />{\alpha _i }<br />$$<br />es fácil ver que $$<br />\operatorname{sgn} \alpha _i = \left( { - 1} \right)^{r_i - 1} <br />$$<br /><br />luego como sgn es un homomorfismo se tiene que $$<br />\operatorname{sgn} \sigma = \prod\limits_{i = 1}^n {\operatorname{sgn} \alpha _i } = \left( { - 1} \right)^{\sum {r_i } - r} = \left( { - 1} \right)^{n - r} <br />$$<br />$ Mensaje modificado por Arkjham el Oct 17 2011, 10:18 PM

Gastón Burrull	Oct 17 2011, 10:28 PM Publicado: #5
Invitado	P2) a) -1 es elemento de orden 2 en (Q-{0},*), un isomorfismo mantiene el orden, pero no hay elementos de orden 2 en (Q,+), qed.

Gastón Burrull	Oct 17 2011, 10:31 PM Publicado: #6
Invitado	4a) El conjunto claramente está en biyección con pot(N), por tanto es no numerable. 4b) No lo son, la suma directa numerable es numerable.

« Posterior · Álgebra Abstracta · Anterior »

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 29th October 2025 - 04:53 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.