E Análisis Real - Foro fmat.cl

Foro fmat.cl > Programa Enseñanza Universitaria > Comunidades Universitarias > Universidad Católica > Análisis Real

E Análisis Real, 1S 2004

Opciones

Cenizas con Most... Cenizas con Mostaza Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 29 2012, 01:27 AM Publicado: #1
Dios Matemático Grupo: Usuario FMAT Mensajes: 465 Registrado: 15-July 11 Miembro Nº: 91.905 Nacionalidad: Universidad: Sexo:	Prof. Alejandro Ramírez. 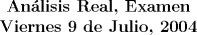$TEX: \begin{center} \bf{Análisis Real, Examen} \\ Viernes 9 de Julio, 2004 \end{center}$ $TEX: $\textbf{Problema 1:}$ Sea $f$ una función en un intervalo $[a,b]$ con derivada continua en $(a,b)$. Si $a<c<d<b$, demuestre que:$ $TEX: 1. $f$ es de variación acotada en $[c,d]$<br /><br />2. Si $T_f(c,d)$ es la variación en el cerrado $[c,d]$, entonces $$\int_c^d \|f'\|(x)dx\leq T_f(c,d)$$$ $TEX: $\textbf{Problema 2:}$ Enuncie y demuestre el Teorema de Dini.<br /><br />$\textbf{Problema 3:}$ Una función $f:[0,1]\to \mathbb{R}$ se dice $\textbf{Hölder continua}$ de orden $\alpha$ si existe una constante $C$ tal que $\|f(x)-f(y)\|\leq C\|x-y\|^{\alpha}$. Defina $$\|\|f\|\|_{\alpha}=\max\{\|f(x)\|\}+\sup \{\dfrac{\|f(x)-f(y)\|}{\|x-y\|^{\alpha}}\}$$<br /><br />Demuestre que si $0<\alpha\leq 1$, el conjunto de funciones $$\{f\in C[0,1]:\|\|f\|\|_{\alpha}\leq 1\}$$<br /><br />es un subconjunto compacto de $C[0,1]$.<br /><br />$\textbf{Problema 4:}$ Sean $X,Y$ espacios métricos donde $X$ es compacto. Sea $f:X\to Y$ una función continua.$ $TEX: 1. Demuestre que $f(X)\subset Y$ es compacto.<br /><br />2. Suponga que $f$ es una biyección entre $X$ y $f(X)$. Demuestre que $f$ es un homeomorfismo.<br /><br />$\textbf{Problema 5:}$ Sea $X$ un espacio métrico completo y $E\subset X$.$ $TEX: 1. Demuestre que si $F\subset E$ es cerrado en $E$ y $E^c$ es denso, entonces $F$ es denso en ninguna parte.<br /><br />2. Demuestre que si $E$ y $E^c$ son densos en $X$, no es posible que cada uno de estos conjuntos se pueda expresar como una unión numerable de cerrados.<br /><br />3. Demuestre que $\mathbb{Q}\cap [0,1]$ no es una intersección numerable de abiertos. <br /><br />4. ¿Existe $f:[0,1]\to [0,1]$ continua en los racionales y discontinua en los irracionales?$ -------------------- He-llo? Could you say that again? More slowly? In a language I understand? Depending on what you said, I might kick your ass!