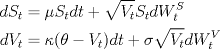|
|
|
|
|
|
|
  |
 Feb 1 2012, 02:36 PM Feb 1 2012, 02:36 PM
Publicado:
#1
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 465 Registrado: 15-July 11 Miembro Nº: 91.905 Nacionalidad:  Universidad:  Sexo:  |
Prof. Mariel Sáez
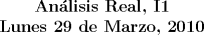 ![TEX: $\textbf{Problema 1:}$ Sea $X=C(\mathbb{R})$ el espacio de las funciones $f:\mathbb{R}\to \mathbb{R}$ continuas. Sea $d_n:X^2\to \mathbb{R}$ definida como $$d_n(f,g)=sup\{|f(t)-g(t)|:t\in [-n,n]\}, \forall f,g\in X$$<br /><br />1. Demuestre que $d_n$ no define una métrica sobre $X$.<br /><br />2. Demuestre que $d:X^2\to \mathbb{R}$ definida como $$d(f,g)=\sum_{n=1}^{\infty} \dfrac{1}{2^n}\dfrac{d_n(f,g)}{1+d_n(f,g)}, \forall f,g\in X$$<br /><br />define una métrica sobre $X$ tal que $d(f,g)\leq 1, \forall f,g\in X$.<br /><br />3. Considere $(\mathbb{R},d_{\mathbb{R}})$ con la distancia $d_{\mathbb{R}}(a,b)=|a-b|$. Sea $\{f_n\}\subset X$ una sucesión y $f\in X$ tal que $f_n\to f$ en $(X,d)$ cuando $n\to \infty$. Demuestre que $f_n(x)\to f(x)$ en $(\mathbb{R},d_{\mathbb{R}})$ cuando $n\to \infty$, $\forall x\in \mathbb{R}$.<br /><br />$\textbf{Problema2:}$ Sea $(X,d)$ un espacio métrico y $A\subset X$. Demuestre que: <br /><br />1.$\overline {\overline{A}}=\overline{A}$.<br /><br />2. $\partial A=\partial (X\setminus A)$.<br /><br />3. $A^{\circ}=\displaystyle \bigcup_{O_{\alpha}\in \mathcal{F}} O_{\alpha}$ donde $\mathcal{F}=\{O:O\subset A, O \ abierto\}$. <br /><br />$\textbf{Problema 3:}$ Considere el espacio $C[0,1]$ de los endomorfismos continuos en $[0,1]$ con la métrica usual inducida por $\mathbb{R}$. Se define sobre $C[0,1]$ la métrica $$d(f,g)=sup\{|f(t)-g(t)|: t\in[0,1]\}, \forall f,g\in C[0,1]$$<br /><br />Sea $\varphi:C[0,1]\to C[0,1]$ la función definida por $$\varphi(f)(t)=\int_0^t sf(s)ds$$<br /><br />1. Demuestre que $\varphi$ está bien definida, es decir, si $f\in C[0,1]$, entonces $\varphi(f)\in C[0,1]$.<br /><br />2. Demuestre que $\varphi:(C[0,1],d)\to (C[0,1],d)$ es continua.<br /><br />3. Demuestre que $\{f\in C[0,1]: \int_0^t sf(s)=e^{-t}\}$ es cerrado en $(C[0,1],d)$.<br /><br />$\textbf{Problema 4:}$ Sea $(X,d_1)$ un espacio métrico completo y $f$ una isometría sobreyectiva de $(X,d_1)$ en $(X,d_2)$. Demuestre que $(X,d_2)$ es completo.](/tex-image/2db70d4c51e6840a33a93588e0b43f5c.png)
-------------------- He-llo? Could you say that again? More slowly? In a language I understand? Depending on what you said, I might kick your ass! |
|
|
|
 Feb 2 2012, 08:40 AM Feb 2 2012, 08:40 AM
Publicado:
#2
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 465 Registrado: 15-July 11 Miembro Nº: 91.905 Nacionalidad:  Universidad:  Sexo:  |
Problema 4:
Sea 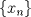 una sucesión de Cauchy en una sucesión de Cauchy en 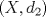 . Como . Como 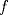 es sobreyectiva, existe una sucesión es sobreyectiva, existe una sucesión 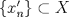 tal que tal que 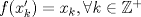 . Como . Como 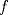 es isometría, entonces es isometría, entonces 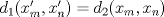 . Como . Como 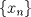 es de Cauchy, entonces es de Cauchy, entonces 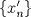 también lo es. Como también lo es. Como 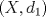 es completo, la sucesión es completo, la sucesión 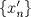 converge a converge a 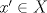 . Sea . Sea 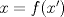 . Por ser . Por ser 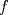 una isometría, se cumple que una isometría, se cumple que 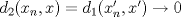 cuando cuando 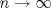 . Por lo tanto . Por lo tanto 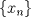 converge a un punto en converge a un punto en 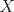 . Por la elección arbitraria de . Por la elección arbitraria de 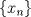 se concluye que toda sucesión de Cauchy en se concluye que toda sucesión de Cauchy en 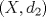 es convergente en el mismo espacio, es decir, es convergente en el mismo espacio, es decir, 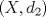 es completo. es completo. 
Mensaje modificado por Cenizas con Mostaza el Feb 2 2012, 08:41 AM -------------------- He-llo? Could you say that again? More slowly? In a language I understand? Depending on what you said, I might kick your ass! |
|
|
|
 Feb 2 2012, 02:40 PM Feb 2 2012, 02:40 PM
Publicado:
#3
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Hola ceniciento xD
-------------------- |
|
|
|
 Feb 2 2012, 03:34 PM Feb 2 2012, 03:34 PM
Publicado:
#4
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 465 Registrado: 15-July 11 Miembro Nº: 91.905 Nacionalidad:  Universidad:  Sexo:  |
Challenge acepted, Kaissa
Problema 3: 1. Sea ![TEX: $f\in C[0,1], x\in[0,1]$](/tex-image/1995ca85d2316b795ba0c0cd46be59bf.png) . Es sencillo ver que . Es sencillo ver que 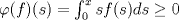 y que y que 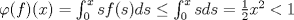 , es decir, , es decir, ![TEX: $\varphi(f)\in B[0,1]$](/tex-image/ae8b0a76866b9847a25aa0f8cd4d66cb.png) . Falta ver que . Falta ver que 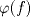 es continua. Dados es continua. Dados  , notar que , notar que 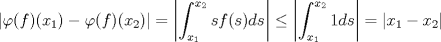 De acá se concluye que 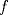 es continua. Por lo tanto es continua. Por lo tanto ![TEX: $\varphi(f)\in C[0,1]$](/tex-image/703b06ba437741bd2d864b60ea94776f.png) . .2. Sean ![TEX: $f_1,f_2\in C[0,1]$](/tex-image/5dac68484e2608fddf274fd89ee7f5a2.png) Si Si ![TEX: $x\in[0,1]$](/tex-image/e38048add0849b21b92031368da3c14c.png) , entonces , entonces 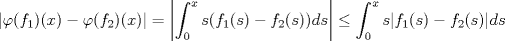 Como 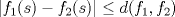 y y 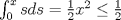 se sigue que se sigue que ![TEX: $|\varphi(f_1)(x)-\varphi(f_2)(x)|\leq \frac{1}{2}d(f_1,f_2)|, \forall x\in[0,1]$](/tex-image/56b39966a3f1e6858c098f3b547c6174.png) . Tomando supremo, se sigue que . Tomando supremo, se sigue que 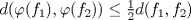 , es decir, , es decir, 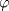 es una contracción y por ende, continua. es una contracción y por ende, continua.3. El conjunto 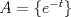 es cerrado por ser un singleton en un espacio métrico. Como es cerrado por ser un singleton en un espacio métrico. Como 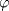 es continua, se sigue que es continua, se sigue que 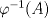 es cerrado. es cerrado. Saludos. Mensaje modificado por Cenizas con Mostaza el Feb 2 2012, 03:38 PM -------------------- He-llo? Could you say that again? More slowly? In a language I understand? Depending on what you said, I might kick your ass! |
|
|
|
 Feb 2 2012, 03:36 PM Feb 2 2012, 03:36 PM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.139 Registrado: 11-June 08 Desde: UK Miembro Nº: 26.837 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Challenge acepted, Kaissa Problema 3: 1. Sea ![TEX: $f\in C[0,1], x\in[0,1]$](/tex-image/1995ca85d2316b795ba0c0cd46be59bf.png) . Es sencillo ver que . Es sencillo ver que 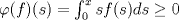 y que y que 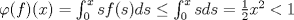 , es decir, , es decir, ![TEX: $\varphi(f)\in B[0,1]$](/tex-image/ae8b0a76866b9847a25aa0f8cd4d66cb.png) . Falta ver que . Falta ver que 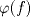 es continua. Dados es continua. Dados  , notar que , notar que 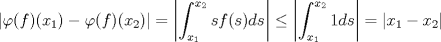 De acá se concluye que 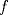 es continua. Por lo tanto es continua. Por lo tanto ![TEX: $\varphi(f)\in C[0,1]$](/tex-image/703b06ba437741bd2d864b60ea94776f.png) . .2. Sean ![TEX: $f_1,f_2\in C[0,1]$](/tex-image/5dac68484e2608fddf274fd89ee7f5a2.png) Si Si ![TEX: $x\in[0,1]$](/tex-image/e38048add0849b21b92031368da3c14c.png) , entonces , entonces 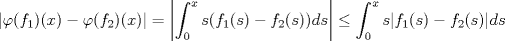 Como 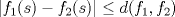 y y 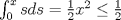 se sigue que se sigue que ![TEX: $|\varphi(f_1)(x)-\varphi(f_2)(x)|\leq \frac{1}{2}d(f_1,f_2)|, \forall x\in[0,1]$](/tex-image/56b39966a3f1e6858c098f3b547c6174.png) . Tomando supremo, se sigue que . Tomando supremo, se sigue que 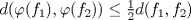 , es decir, , es decir, 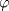 es una contracción y por ende, continua. es una contracción y por ende, continua.3. El conjunto 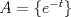 es cerrado por ser un singleton. Como es cerrado por ser un singleton. Como 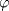 es continua, se sigue que es continua, se sigue que 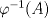 es cerrado. es cerrado.Saludos. Los singleton son cerrados por que el espacio es metrico :-p, luego hausdorff -------------------- blep
|
|
|
|
 Feb 2 2012, 03:39 PM Feb 2 2012, 03:39 PM
Publicado:
#6
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 465 Registrado: 15-July 11 Miembro Nº: 91.905 Nacionalidad:  Universidad:  Sexo:  |
Los singleton son cerrados por que el espacio es metrico :-p, luego hausdorff Editado, gracias. Se me había pasado por alto. -------------------- He-llo? Could you say that again? More slowly? In a language I understand? Depending on what you said, I might kick your ass! |
|
|
|
 Feb 2 2012, 03:42 PM Feb 2 2012, 03:42 PM
Publicado:
#7
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad:  Colegio/Liceo:  Sexo:  |
te contaron lo que significa esa integral?
-------------------- |
|
|
|
 Feb 2 2012, 03:47 PM Feb 2 2012, 03:47 PM
Publicado:
#8
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 465 Registrado: 15-July 11 Miembro Nº: 91.905 Nacionalidad:  Universidad:  Sexo:  |
te contaron lo que significa esa integral? La verdad no Mensaje modificado por Cenizas con Mostaza el Feb 2 2012, 03:48 PM -------------------- He-llo? Could you say that again? More slowly? In a language I understand? Depending on what you said, I might kick your ass! |
|
|
|
 Feb 2 2012, 03:54 PM Feb 2 2012, 03:54 PM
Publicado:
#9
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Para que te intereses, son esas transformaciones raras para usar en espacios de distribuciones.
-------------------- |
|
|
|
 Feb 2 2012, 05:38 PM Feb 2 2012, 05:38 PM
Publicado:
#10
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Soy el único al que le parece raro el conjunto de 3c? A mi parecer, es vacío.
-------------------- |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 29th October 2025 - 08:21 AM |













![TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]](./tex/e0e88dba678ca3ead120b088f41191b2.png)