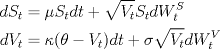I3 Análisis Real - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa Enseñanza Universitaria > Comunidades Universitarias > Universidad Católica > Análisis Real

Reply to this topic

Start new topic

I3 Análisis Real, 1S 2010

Cenizas con Most... Cenizas con Mostaza Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 1 2012, 02:38 PM Publicado: #1
Dios Matemático Grupo: Usuario FMAT Mensajes: 465 Registrado: 15-July 11 Miembro Nº: 91.905 Nacionalidad: Universidad: Sexo:	Prof. Mariel Sáez $TEX: \begin{center} \bf{Análisis Real, I3} \\ Lunes 7 de Junio, 2010 \end{center}$ $TEX: $\textbf{Problema 1:}$ Sea $(X,d)$ un espacio métrico completo. Un punto $x\in X$ se dice aislado si $\exists r>0$ tal que $B(x;r)=\{x\}$. Demuestre que si $X$ no tiene puntos aislados entonces $X$ no es numerable.<br /><br />$\textbf{Problema 2:}$ Demuestre que el espacio $$\ell^p=\{\{a_n\}\subset \mathbb{R}:\sum_{n=1}^{\infty} \|a_n\|^p<\infty\}$$ con $p>1$ es un espacio vectorial sobre $\mathbb{R}$ que no posee dimensión finita.<br /><br />$\textbf{Problema 3:}$ Sean $(X,d_X)$, $(Y,d_Y)$ espacios métricos compactos. Se define en $X\times Y$ la métrica producto $$d_{X\times Y}((x_1,y_2), (x_2,y_2))=d_X(x_1,x_2)+d_Y(y_1,y_2)$$<br /><br />Demuestre que el conjunto $$A=\{\sum_{i=1}^n f_i(x)g_i(y)\in C(X\times Y, \mathbb{R}): n\in \mathbb{Z}^+, f_i\in C(X,\mathbb{R}), g_i\in C(Y,\mathbb{R})\}$$<br /><br />es denso en $C(X\times Y, \mathbb{R})$ con la norma del supremo.<br /><br />$\textbf{Problema 4:}$ Sea $(X,\|\|\cdot\|\|)$ un espacio normado. <br /><br />1. Demuestre que $\forall x_0\in X$ se cumple que $$\|\|x_0\|\|=max\{\|f(x_0)\|: f\in X^, \|\|f\|\|\leq 1\}$$<br /><br />2. Sean $x_0\in X$ y $\{x_n\}\subset X$ una sucesión tal que $\forall f\in X^$ se cumple que $f(x_n)\to f(x_0)$ cuando $n\to \infty$. Demuestre que $\|\|x_0\|\|\leq \liminf_{n\to \infty} \|\|x_n\|\|$.$ -------------------- He-llo? Could you say that again? More slowly? In a language I understand? Depending on what you said, I might kick your ass!

Abu-Khalil Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 1 2012, 08:44 PM Publicado: #2
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	P1 $TEX: \noindent Supongamos que $X$ es numerable y sea $(x_n)_{n\in\mathbb N}$ una numeración de éste. Si ningún $x_n$ es aislado, entonces, para cada $n\in\mathbb N$, el conjunto $F_n=\{x_n\}$ es un cerrado de interior vacío y por ende, denso en ninguna parte. La contradiccón sigue del hecho que $X=\bigcup_{n\in\mathbb N}F_n$ y el teorema de categorías de Baire.$\quad\square$$ P2 $TEX: \noindent Si $l^p$ fuese de dimensión finita, entonces su bola unitaria sería compacta. Sin embargo, si se considera la sucesión de vectores canónicos $(e_n)_{n\in\mathbb N}$, se tiene que<br />$$\\|e_n-e_m\\|=2,\quad \forall n\ne m,$$<br />y por ende, dicha sucesión no puede subsucesiones de Cauchy.<br />$ -------------------- ~milopez $TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]$ $TEX: <br />\begin{equation}\begin{aligned}<br />dS_t&=\mu S_t dt+\sqrt{V_t}S_t dW^S_t\\<br />dV_t&=\kappa(\theta-V_t)dt+\sigma\sqrt{V_t} dW^V_t\\<br />\end{aligned}\end{equation}<br />$ $TEX: <br />$$\mathbb A^{\text U}_M(N)$$<br />$

« Posterior · Análisis Real · Anterior »

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 30th April 2025 - 10:03 AM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.