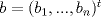|
|
|
|
|
|
|
  |
 Oct 12 2012, 06:43 PM Oct 12 2012, 06:43 PM
Publicado:
#1
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 465 Registrado: 15-July 11 Miembro Nº: 91.905 Nacionalidad:  Universidad:  Sexo:  |
Prof. Martín Chuaqui
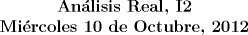   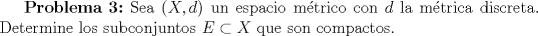  Hint para el problema 2: Mensaje modificado por Cenizas con Mostaza el Oct 12 2012, 10:17 PM -------------------- He-llo? Could you say that again? More slowly? In a language I understand? Depending on what you said, I might kick your ass! |
|
|
|
 Oct 12 2012, 06:44 PM Oct 12 2012, 06:44 PM
Publicado:
#2
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 465 Registrado: 15-July 11 Miembro Nº: 91.905 Nacionalidad:  Universidad:  Sexo:  |
Problema 2:

Mensaje modificado por Cenizas con Mostaza el Oct 12 2012, 06:46 PM -------------------- He-llo? Could you say that again? More slowly? In a language I understand? Depending on what you said, I might kick your ass! |
|
|
|
 Oct 12 2012, 06:56 PM Oct 12 2012, 06:56 PM
Publicado:
#3
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 465 Registrado: 15-July 11 Miembro Nº: 91.905 Nacionalidad:  Universidad:  Sexo:  |
Problema 4:
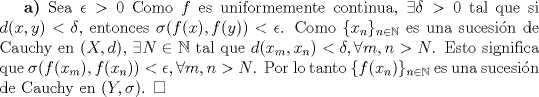  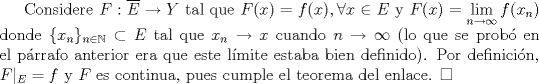 Saludos, espero que este bien Mensaje modificado por Cenizas con Mostaza el Oct 12 2012, 07:45 PM -------------------- He-llo? Could you say that again? More slowly? In a language I understand? Depending on what you said, I might kick your ass! |
|
|
|
 Oct 12 2012, 07:35 PM Oct 12 2012, 07:35 PM
Publicado:
#4
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Encuentro bueno el nivel, bastante medido con los regalos del P1 y el P3
-------------------- |
|
|
|
 Oct 17 2012, 12:31 AM Oct 17 2012, 12:31 AM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.767 Registrado: 21-January 08 Desde: Santiago - Ancud Miembro Nº: 14.865 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Problema 3:
 Alguien que mate el problema 1. -------------------- Estudia para superarte a ti mismo, no al resto. |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 29th October 2025 - 08:18 AM |





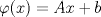 , donde
, donde 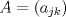 y
y