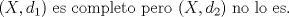|
|
|
|
|
|
|
  |
 Apr 3 2013, 10:07 PM Apr 3 2013, 10:07 PM
Publicado:
#1
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 465 Registrado: 15-July 11 Miembro Nº: 91.905 Nacionalidad:  Universidad:  Sexo:  |
Prof. Matías Courdurier.
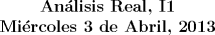 ![TEX: $\textbf{Problema 1:}$ Sea $X=C([0,1];\mathbb{R})$ y $A=\{f\in X:f(0)=0\}$. Para $f,g\in X$, defina $d(f,g)=\displaystyle \sup_{x\in[0,1]} |f(x)-g(x)|$ y $\rho(f,g)=\displaystyle \int_0^1 |f(x)-g(x)|dx$. <br /><br />$\textbf{a)}$ Calcule $\overline{A}$, $int(A)$ en el espacio métrico $(X,d)$.<br /><br />$\textbf{b)}$ Calcule $\overline{A}$, $int(A)$ en el espacio métrico $(X,\rho)$.](/tex-image/dcd48544e47fe420b027755673b1b98e.png) ![TEX: $\textbf{Problema 2:}$ $\textbf{a)}$ Sea $(Y,\rho)$ un espacio métrico, $X$ un conjunto y considere $f:X\to Y$ una función. Defina $d:X\times X\to \mathbb{R}$ como $d(x,y)=\rho(f(x),f(y))$<br /><br />$\textbf{i)}$ ¿Cuáles son las condiciones necesarias y suficientes para que $d$ sea una métrica en $X$?<br /><br />$\textbf{ii)}$ Si las condiciones de $\textbf{i)}$ se satisfacen, demuestre que $f:(X,d)\to (Y,\rho)$ es continua. ¿Cuáles son las condicione necesarias y suficientes para que $f:(X,d)\to (Y,\rho)$ sea una isometría?<br /><br />$\textbf{b)}$ Sea $X=(0,1]$. Encuentre dos métricas $d_1$ y $d_2$ en $X$ que satisfacen las siguientes dos propiedades a la vez.](/tex-image/6c9665ff74180197d335108c2c5ab27f.png) ![TEX: $\textbf{Problema 3:}$ En el conjunto $C([0,1];\mathbb{R})$, considere la métrica $d(f,g)=\displaystyle \sup_{x\in [0,1]} |f(x)-g(x)|$. Demuestre que $(C([0,1];\mathbb{R}),d)$ es un espacio métrico completo.](/tex-image/e4a92d153208684e7ab0eeefd6fed0f6.png) ![TEX: $\textbf{Problema 4:}$ Demuestre que existe una única función $f\in C^2([0,1];[0,1])$ que satisface <br /><br />$f''(x)-e^{-x}f(x)=0$<br /><br />$f(0)=f'(0)=0$](/tex-image/9080adaf0b9a8f7cbe726eefa8bb87dd.png)
-------------------- He-llo? Could you say that again? More slowly? In a language I understand? Depending on what you said, I might kick your ass! |
|
|
|
 Apr 4 2013, 05:29 AM Apr 4 2013, 05:29 AM
Publicado:
#2
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 465 Registrado: 15-July 11 Miembro Nº: 91.905 Nacionalidad:  Universidad:  Sexo:  |
![TEX: $\textbf{Problema 1:}$ Sea $X=C([0,1];\mathbb{R})$ y $A=\{f\in X:f(0)=0\}$. Para $f,g\in X$, defina $d(f,g)=\displaystyle \sup_{x\in[0,1]} |f(x)-g(x)|$ y $\rho(f,g)=\displaystyle \int_0^1 |f(x)-g(x)|dx$. <br /><br />$\textbf{a)}$ Calcule $\overline{A}$, $int(A)$ en el espacio métrico $(X,d)$.<br /><br />$\textbf{b)}$ Calcule $\overline{A}$, $int(A)$ en el espacio métrico $(X,\rho)$.](/tex-image/dcd48544e47fe420b027755673b1b98e.png) a) Se probará que 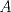 es cerrado. Sea es cerrado. Sea 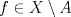 . Luego . Luego 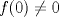 . Si . Si 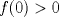 , considere , considere 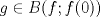 . Luego, . Luego, 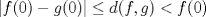 , de donde , de donde 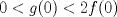 . Esto significa que . Esto significa que 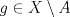 , luego , luego 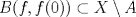 . Si . Si 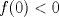 , se cumple que , se cumple que 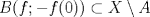 . Se cumple entonces que . Se cumple entonces que 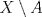 es abierto y en consecuencia es abierto y en consecuencia  Se probará que 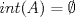 . Si . Si 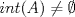 , entonces , entonces 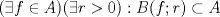 Considere 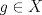 tal que tal que ![TEX: $g(x)=f(x)+\dfrac{1}{2}r,\forall x\in[0,1]$](/tex-image/0e73a86f33272d0d76e72fcc89a5cd81.png) . Note que . Note que 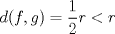 , i.e, , i.e, 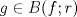 . Pero . Pero 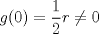 , lo que significa que , lo que significa que 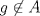 . Esto contradice que . Esto contradice que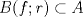 . Por lo tanto . Por lo tanto 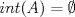 . .b) Se probará que 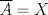 . Sea . Sea 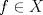 . Note que . Note que 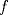 es continua en un compacto en es continua en un compacto en 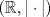 , así que es acotada, i.e, , así que es acotada, i.e, ![TEX: $(\exists C>0)<img src="style_emoticons/default/sad.gif" style="vertical-align:middle" emoid=":(" border="0" alt="sad.gif" />x\in[0,1])\Rightarrow |f(x)|\leq C$](/tex-image/89fa62f2c4763cce3e3dd98593fae56c.png) . Esto significa que . Esto significa que ![TEX: $\displaystyle \int_0^x |f(t)|dt\leq Cx,\forall x\in[0,1]$](/tex-image/621b830edc72993a12b4dcde85ad6d3e.png) . Dado . Dado 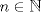 , defina , defina![TEX: \[f_n(x)=\begin{cases}\begin{tabular}{c c c}<br />$nf(\dfrac{1}{n})x,$&si&$0\leq x\leq \dfrac{1}{n}$;\\<br />\\<br />$f(x)$,&si&$\dfrac{1}{n}<x\leq 1$.<br />\end{tabular}\end{cases}\]](/tex-image/d343ff2c85e1594a4ee16e973841623e.png) Note que 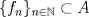 . Se probará que . Se probará que 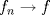 en en 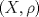 . Vea que . Vea que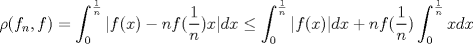 Como 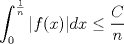 y y 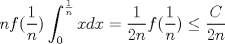 , se sigue que , se sigue que 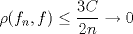 cuando cuando 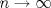 . Con esto queda demostrado que . Con esto queda demostrado que 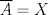 . .Se probará que 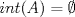 . Si . Si 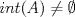 , entonces , entonces 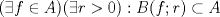 Considere 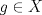 tal que tal que ![TEX: $g(x)=f(x)+\dfrac{1}{2}r,\forall x\in[0,1]$](/tex-image/76e958d244fa1e786e710d3227eca8c7.png) . Note que . Note que 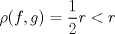 , i.e, , i.e, 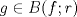 . Pero . Pero 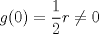 , lo que significa que , lo que significa que 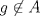 . Esto contradice que . Esto contradice que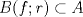 . Por lo tanto . Por lo tanto 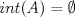 . .
-------------------- He-llo? Could you say that again? More slowly? In a language I understand? Depending on what you said, I might kick your ass! |
|
|
|
 Apr 13 2013, 10:36 PM Apr 13 2013, 10:36 PM
Publicado:
#3
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 465 Registrado: 15-July 11 Miembro Nº: 91.905 Nacionalidad:  Universidad:  Sexo:  |
2.b) Considere
![TEX: $d_1,d_2:(0,1]\times (0,1]\to \mathbb{R}$](/tex-image/cc1268334132098ae4775f662db3d548.png) tales que tales que ![TEX: $\forall x,y\in (0,1]$](/tex-image/897789239b8120791cc4fe096df33267.png) se cumpla que se cumpla que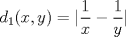 y y 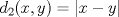 Sea ![TEX: $\{x_n\}_{n\in \mathbb{N}}\subset (0,1]$](/tex-image/d664fddef5695756e209c4a870925fde.png) . Suponga que . Suponga que 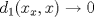 . Como . Como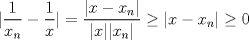 se tiene que 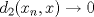 . Por otra parte, si . Por otra parte, si 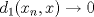 , entonces , entonces 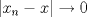 . Como la función . Como la función 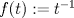 es continua en es continua en 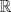 dotado de la métrica usual, entonces dotado de la métrica usual, entonces 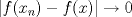 , es decir, , es decir, 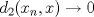 . Con esto se prueba que . Con esto se prueba que 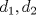 satisfacen la primera condición pedida. satisfacen la primera condición pedida.Sea ![TEX: $\{x_n\}_{n\in \mathbb{N}}\subset (0,1]$](/tex-image/3543ebce5372983036b74911c3b611af.png) una sucesión de Cauchy en una sucesión de Cauchy en ![TEX: $((0,1],d_1)$](/tex-image/131be330a13f4ef90e9d03a619b1bc01.png) . Entonces la sucesión . Entonces la sucesión 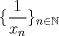 es de Cauchy en es de Cauchy en 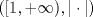 . Al ser . Al ser 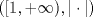 completo (subconjunto cerrado de un completo con la métrica inducida), se tiene que completo (subconjunto cerrado de un completo con la métrica inducida), se tiene que 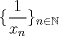 converge a converge a 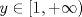 . Note que . Note que ![TEX: $y^{-1}\in (0,1]$](/tex-image/ef56ab50be5fb2dfca674429299d754a.png) . Por la continuidad de . Por la continuidad de 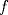 , se sigue que , se sigue que 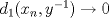 , i.e, , i.e, 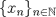 es convergente. Por lo tanto es convergente. Por lo tanto ![TEX: $((0,1],d_1)$](/tex-image/a14a3c235f8ac13d3f017d783ec14d67.png) es completo. es completo. Para ver que ![TEX: $((0,1],d_2)$](/tex-image/7e06edabb68f948156eaf824222bef93.png) no es completo, basta ver que no es completo, basta ver que 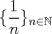 es de Cauchy (pues es de Cauchy (pues 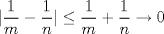 cuando cuando 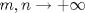 ), pero ), pero ![TEX: $\dfrac{1}{n}\to 0\not \in (0,1]$](/tex-image/3da976bc665eb61e80608e1312d3957d.png) cuando cuando 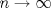 . Por lo tanto . Por lo tanto ![TEX: $((0,1],d_2)$](/tex-image/15a8a8a9c3272f0ec447c6f0f36d2f99.png) no es completo. no es completo. 
-------------------- He-llo? Could you say that again? More slowly? In a language I understand? Depending on what you said, I might kick your ass! |
|
|
|
 Apr 14 2013, 08:24 AM Apr 14 2013, 08:24 AM
Publicado:
#4
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Problema 3, acá:
Teorema 4.23 (como es la típica "demostración de libro" es mejor postear un link que hacerla de nuevo) -------------------- |
|
|
|
 Apr 14 2013, 08:33 AM Apr 14 2013, 08:33 AM
Publicado:
#5
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 465 Registrado: 15-July 11 Miembro Nº: 91.905 Nacionalidad:  Universidad:  Sexo:  |
Problema 3, acá: Teorema 4.23 (como es la típica "demostración de libro" es mejor postear un link que hacerla de nuevo) Sí, de hecho el problema 3 salió en la tarea 1 también.... y el problema 4 es un problema típico del teorema del punto fijo de Banach. -------------------- He-llo? Could you say that again? More slowly? In a language I understand? Depending on what you said, I might kick your ass! |
|
|
|
 Nov 2 2014, 01:38 AM Nov 2 2014, 01:38 AM
Publicado:
#6
|
|
 Maestro Matemático Grupo: Team Ensayos FMAT Mensajes: 114 Registrado: 4-March 09 Desde: Ñuñoa Miembro Nº: 44.042 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
![TEX: 4)Tomando la expresión integral<br />$$f(x) = \int_0^x \int_0^y f(t) e^{-t}dtdy $$ <br />Veamos primero que esta bien definida.<br />Sea $T: (X,d) \to (X,d) , f \in X, x\in [0,1] $<br />$$ Tf(x) = \int_0^x \int_0^y f(t) e^{-t}dtdy $$<br />Acotando por el supremo<br />$$ Tf(x) = \int_0^x \int_0^y f(t) e^{-t}dtdy \leq sup_{x \in [0,1]} e^{-x} f(x) \int_0^x \int_0^y dtdy \leq sup_{x \in [0,1]} e ^0 1 \int_0^x \int_0^y dtdy $$ $$\leq sup_{x \in [0,1]} \frac{x^2}{2} \leq \frac{1}{2} < 1$$<br />Por ende es cerrado, y $Tf(x) $ esta bien definda en $[0,1] \to [0,1] $<br /><br />Ahora busquemos la contracción<br />Sea $f,g \in X $, $f: [0,1] \to [0,1] $, y $T(f(x)) $ definida anteriormente,y de manera análoga al anterior acotamos.<br /><br />$$d(T(f(x)),T(g(x))) \leq sup_{x \in [0,1]} \int_0^x \int_0^y |f(t)-g(t)| e^{-t}dtdy \leq $$ $$ sup_{x \in [0,1]}|f(x)-g(x)|e^{-x} \int_0^x \int_0^y dtdy \leq sup_{x \in [0,1]} |f(x)-g(x)|e^{-0} \frac{x^2}{2}<br />$$ $$\leq sup_{x \in [0,1]} |f(x)-g(x)|\frac{1}{2} $$<br /><br />Como $K=\frac{1}{2} $ es una contracción, y ademas una función uniformemente continua. Luego, por teorema del punto fijo de Banach existe una única solución de $f(x)$.](/tex-image/c4154d3ee673f37aa98d27ad54fa5c59.png)
Mensaje modificado por GmHernan el Nov 2 2014, 01:39 AM -------------------- |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 29th October 2025 - 08:20 AM |





![TEX: Para toda sucesión $\{x_n\}_{n\in \mathbb{N}}\subset (0,1]$:$[d_1(x_n,x)\to 0]\Leftrightarrow [d_2(x_n,x)\to 0]$](/tex-image/33154d997013ec37c5fe32f069f4d96c.png)