|
|
|
|
|
|
|
  |
 Apr 14 2013, 09:27 AM Apr 14 2013, 09:27 AM
Publicado:
#1
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 465 Registrado: 15-July 11 Miembro Nº: 91.905 Nacionalidad:  Universidad:  Sexo:  |
Prof. Olivier Bourget.
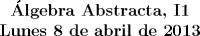 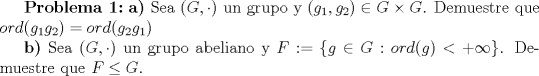 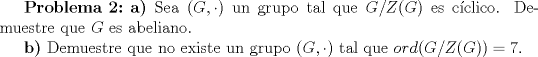  Mensaje modificado por Cenizas con Mostaza el Apr 14 2013, 03:07 PM -------------------- He-llo? Could you say that again? More slowly? In a language I understand? Depending on what you said, I might kick your ass! |
|
|
|
 Apr 14 2013, 10:24 AM Apr 14 2013, 10:24 AM
Publicado:
#2
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Olivier dicta álgebra!
-------------------- |
|
|
|
 Apr 14 2013, 10:48 AM Apr 14 2013, 10:48 AM
Publicado:
#3
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 465 Registrado: 15-July 11 Miembro Nº: 91.905 Nacionalidad:  Universidad:  Sexo:  |
Olivier dicta álgebra! Sí D: Postearé la solución de los problemas 1a y 2b (que son cortitas). Mi solución original del 1a era formando una biyección  , pero Gostan me enseñó una más bonita D: que quiero compartir. (Creo que debí estudiar más) , pero Gostan me enseñó una más bonita D: que quiero compartir. (Creo que debí estudiar más)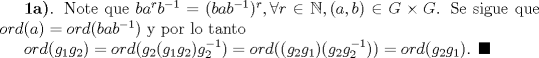 
Mensaje modificado por Cenizas con Mostaza el Apr 14 2013, 03:07 PM -------------------- He-llo? Could you say that again? More slowly? In a language I understand? Depending on what you said, I might kick your ass! |
|
|
|
 Apr 14 2013, 11:32 AM Apr 14 2013, 11:32 AM
Publicado:
#4
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 832 Registrado: 11-September 07 Desde: París, Francia Miembro Nº: 10.056 Nacionalidad:  Sexo:  |
|
|
|
|
 Apr 14 2013, 11:55 AM Apr 14 2013, 11:55 AM
Publicado:
#5
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 465 Registrado: 15-July 11 Miembro Nº: 91.905 Nacionalidad:  Universidad:  Sexo:  |
Edit.. taba drogao
Mensaje modificado por Cenizas con Mostaza el Apr 14 2013, 03:07 PM -------------------- He-llo? Could you say that again? More slowly? In a language I understand? Depending on what you said, I might kick your ass! |
|
|
|
 Apr 14 2013, 12:04 PM Apr 14 2013, 12:04 PM
Publicado:
#6
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 832 Registrado: 11-September 07 Desde: París, Francia Miembro Nº: 10.056 Nacionalidad:  Sexo:  |
|
|
|
|
 May 22 2013, 12:21 AM May 22 2013, 12:21 AM
Publicado:
#7
|
|
|
Dios Matemático Supremo Grupo: Super Moderador Mensajes: 2.065 Registrado: 25-May 08 Desde: Pelotillehue Miembro Nº: 24.463 |
1a.
http://www.fmat.cl/index.php?showtopic=62002&hl= 1b. 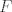 es no vacío. Sean es no vacío. Sean  y y  en en 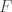 . Puesto que . Puesto que 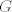 es abeliano y es abeliano y 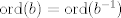 , , 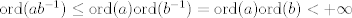 y sería. y sería.2a es clásico. Haga 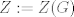 y supóngase y supóngase 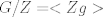 . Sean . Sean  y y  en en 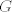 . Puesto que . Puesto que 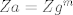 y y 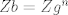 para algunos enteros para algunos enteros  y y  , se sigue que , se sigue que 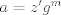 y y 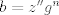 para algunos para algunos 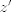 y y 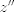 en en 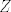 . Ergo, . Ergo, 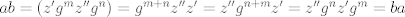 . . 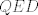 3. http://www.fmat.cl/index.php?showtopic=51156 -------------------- "Please forget everything you have learned in school; for you haven't learned it... Please keep in mind at all times the corresponding portions of your school curriculum; for you haven't actually forgotten them." -- E. Landau
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 29th October 2025 - 04:55 PM |












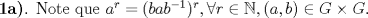
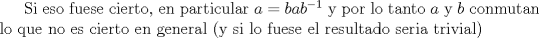
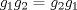 y el ejercicio pierde sentido.
y el ejercicio pierde sentido.
