|
|
|
|
|
|
|
  |
 May 3 2015, 11:00 PM May 3 2015, 11:00 PM
Publicado:
#1
|
|
 Dios Matemático Grupo: Moderador Mensajes: 269 Registrado: 30-August 10 Desde: Santiago, Chile Miembro Nº: 76.269 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
I1 Álgebra Abstracta 1 Primer Semestre 2015 Problema 1. Sean 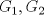 dos grupos y dos grupos y 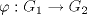 un morfismo de grupos. un morfismo de grupos.a. Mostrar que si 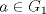 tiene orden finito tiene orden finito 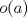 , , 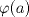 tiene orden finito y tiene orden finito y 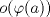 divide a divide a 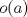 b. Que sucede si 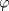 es inyectiva? es inyectiva?c. Determinar los morfimos de grupos (aditivos) 1. De 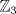 en en 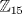 2. De 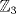 en en 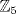 Problema 2. Sean 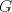 grupo y grupo y 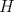 subgrupo de G generado por el conjunto de todos los elementos de la forma subgrupo de G generado por el conjunto de todos los elementos de la forma 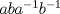 con con 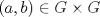 . Mostrar que: . Mostrar que:(a) H es un subgrupo normal de G. (b) 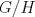 es un grupo abeliano. es un grupo abeliano.© Si N es un subgurpo normal de 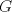 tal que tal que 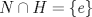 , entonces , entonces 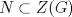 . .Problema 3. Sean 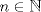 y y 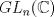 el grupo (multiplicativo) de todas las matrices de el grupo (multiplicativo) de todas las matrices de 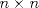 invertibles con coeficientes complejos. Calcular su centro. invertibles con coeficientes complejos. Calcular su centro.Tiempo: 2 horas. -------------------- Estudiante Instituto Nacional General José Miguel Carrera IV Medio(2013) 17 años. Estaba Jesús predicando en el monte Sinaí y dijo a sus discípulos: y = ax² + bx + c ¿Y eso qué es? Dijo uno de los discípulos. A lo que Jesús respondió: ¡Una parábola !  |
|
|
|
 May 3 2015, 11:44 PM May 3 2015, 11:44 PM
Publicado:
#2
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 182 Registrado: 18-February 13 Desde: Santiago Miembro Nº: 115.462 Nacionalidad:  Universidad:  Sexo:  |
P1.a) Sea
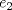 el neutro de el neutro de 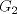 . Como . Como 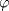 es homomorfismo, es homomorfismo, 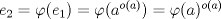 . Luego . Luego 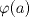 tiene orden finito y claramente tiene orden finito y claramente 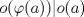 . Iba a decir que esto es obvio ya que son los mismos, pero me di cuenta que no, nada me asegura que . Iba a decir que esto es obvio ya que son los mismos, pero me di cuenta que no, nada me asegura que 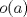 es el orden de es el orden de 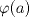 , puede ser un múltiplo. Con esto me tinca que si es monomorfismo entonces son iguales xP mañana lo intento, le estoy sacando el poto a la jeringa con electro :c , puede ser un múltiplo. Con esto me tinca que si es monomorfismo entonces son iguales xP mañana lo intento, le estoy sacando el poto a la jeringa con electro :c
-------------------- |
|
|
|
 May 4 2015, 06:36 AM May 4 2015, 06:36 AM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 736 Registrado: 3-December 12 Miembro Nº: 113.971 Nacionalidad:  Universidad:  Sexo:  |
Edit: Olivier Bourget
Mensaje modificado por Lichiel el May 4 2015, 07:49 PM --------------------    Quiero plata |
|
|
|
 May 4 2015, 07:09 PM May 4 2015, 07:09 PM
Publicado:
#4
|
|
|
Dios Matemático Grupo: Usuario FMAT Mensajes: 409 Registrado: 13-July 12 Desde: Santiago Miembro Nº: 108.957 Nacionalidad:  Colegio/Liceo:  Sexo:  |
una consulta quien esta dando este curso?
-------------------- Kaissa Es ICM!
|
|
|
|
 May 5 2015, 01:35 PM May 5 2015, 01:35 PM
Publicado:
#5
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 5 Registrado: 5-May 15 Miembro Nº: 137.512 Nacionalidad:  Colegio/Liceo:  Sexo:  |
P2) a)
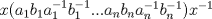 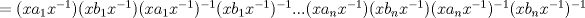 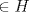 b) Como 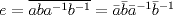 se tiene se tiene 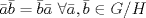 c) 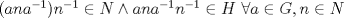 , luego , luego 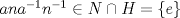 de donde de donde 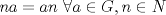 y por lo tanto y por lo tanto 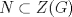
|
|
|
|
 May 5 2015, 01:55 PM May 5 2015, 01:55 PM
Publicado:
#6
|
|
 Dios Matemático Supremo Grupo: Colaborador Silver Mensajes: 1.374 Registrado: 3-January 13 Desde: Santiago Miembro Nº: 114.680 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
¿Cuantos kaissa hay?
--------------------   Mi nombre es Juan Pablo |
|
|
|
 May 5 2015, 02:40 PM May 5 2015, 02:40 PM
Publicado:
#7
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 5 Registrado: 5-May 15 Miembro Nº: 137.512 Nacionalidad:  Colegio/Liceo:  Sexo:  |
|
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 29th October 2025 - 04:57 PM |













![TEX: \[<br />\pi = \left( {\frac{{\sqrt 8 }}<br />{{9801}}\sum\limits_{n = 0}^\infty {\frac{{\left( {4n} \right)!(1103 + 26390n)}}<br />{{(n!)^4 396^{4n} }}} } \right)^{ - 1} <br />\]<br />](/tex-image/de896cbef0f0eca198651d4c1a35a1e4.png)
 [color="#0000FF"][/color]
[color="#0000FF"][/color]