|
|
|
|
|
|
|
  |
 Mar 13 2021, 11:35 AM Mar 13 2021, 11:35 AM
Publicado:
#1
|
|
|
Maestro Matemático Grupo: Usuario FMAT Mensajes: 134 Registrado: 28-March 14 Miembro Nº: 128.100 Nacionalidad:  Sexo:  |
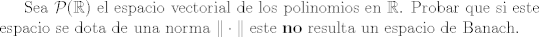
-------------------- Hago clases particulares (activo 2024).
Cualquier consulta por MP. |
|
|
|
 Mar 15 2021, 05:10 PM Mar 15 2021, 05:10 PM
Publicado:
#2
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 119 Registrado: 1-March 13 Desde: Santiago Miembro Nº: 115.656 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Usaré la siguiente versión del Teorema de Categorización de Baire: Si
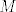 es un espacio métrico completo, entonces es un espacio métrico completo, entonces 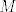 no se puede escribir como la unión numerable de conjuntos cerrados de interior vacío. no se puede escribir como la unión numerable de conjuntos cerrados de interior vacío. Supongamos por contradicción que existe una norma  tal que tal que 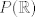 es de Banach. es de Banach.Definamos 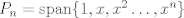 . Notamos que . Notamos que 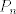 son subespacios de dimensión finita de son subespacios de dimensión finita de 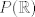 . Como son de dimensión finita, son completos y por lo tanto, cerrados. Además, . Como son de dimensión finita, son completos y por lo tanto, cerrados. Además, 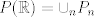 . Así, si probamos que . Así, si probamos que 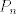 tiene interior vacío, tendríamos una contradicción en virtud del teorema anterior. Para probar que efectivamente tienen interior vacío, supongamos lo contrario:sea tiene interior vacío, tendríamos una contradicción en virtud del teorema anterior. Para probar que efectivamente tienen interior vacío, supongamos lo contrario:sea 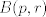 una bola abierta de centro el polinomio una bola abierta de centro el polinomio 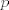 y radio y radio  , contenida en , contenida en 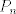 . Sea . Sea 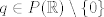 . Entonces . Entonces 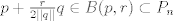 . Finalmente, como . Finalmente, como 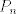 es subespacio, es subespacio, ![TEX: $q=\frac{2||q||}{r}([p+\frac{r}{2||q||}q]-p) \in P_{n}$](/tex-image/053c00a9db2e01233bbc6694437ad406.png) . Esto dice que . Esto dice que 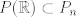 , lo cual es absurdo. Por lo tanto, , lo cual es absurdo. Por lo tanto, 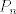 tienen interior vacío. Por lo dicho anteriormente, esto implica el resultado buscado. tienen interior vacío. Por lo dicho anteriormente, esto implica el resultado buscado.
--------------------  |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 29th October 2025 - 09:22 PM |









