|
|
|
|
|
|
|
  |
 Nov 16 2005, 09:43 PM Nov 16 2005, 09:43 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
19ª OLIMPIADA IBEROAMERICANA DE MATEMÁTICAS Problema 1: Deben colorearse casillas de un tablero de Castellón, España, 2004 Primera Prueba: Martes 21 de Septiembre 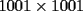 , de manera que: , de manera que:
Problema 2: Considere (fijos en el plano) una circunferencia, y un punto 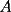 exterior a ella. Sea exterior a ella. Sea 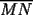 un diámetro variable. Encuentre el LG del circuncentro del un diámetro variable. Encuentre el LG del circuncentro del 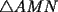 al variar al variar 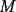 . .Problema 3: Sean 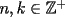 tales que: o bien tales que: o bien  es impar, o bien es impar, o bien 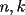 son ambos pares. Pruebe que existen son ambos pares. Pruebe que existen 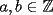 tales que: tales que:
Segunda Prueba: Miércoles 22 de Septiembre Problema 4: Determine todos los pares 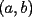 , donde , donde 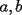 son naturales de dos dígitos, tales que son naturales de dos dígitos, tales que 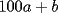 y y 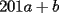 son cuadrados perfectos de cuatro dígitos. son cuadrados perfectos de cuatro dígitos.Problema 5: Dado un 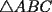 escaleno, se llaman escaleno, se llaman 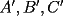 los puntos de intersección de las bisectrices de los puntos de intersección de las bisectrices de 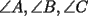 , respectivamente, con el lado opuesto que corresponda. Sea , respectivamente, con el lado opuesto que corresponda. Sea 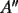 el punto de corte de el punto de corte de 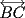 con la mediatriz de con la mediatriz de 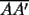 . Los puntos . Los puntos 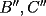 se definen similarmente. Pruebe que se definen similarmente. Pruebe que 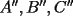 son colineales. son colineales.Problema 6: Para un conjunto 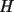 de puntos en el plano, se dice que un punto de puntos en el plano, se dice que un punto 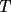 del plano es un punto de corte de del plano es un punto de corte de 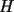 si existen puntos si existen puntos 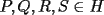 , distintos, tales que las rectas , distintos, tales que las rectas 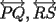 son distintas y se cortan en son distintas y se cortan en 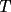 . Dado un conjunto finito . Dado un conjunto finito 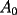 de puntos en el plano, se construye la sucesión de puntos en el plano, se construye la sucesión 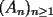 de conjuntos de puntos en el plano, por medio de la siguiente regla: Para cada de conjuntos de puntos en el plano, por medio de la siguiente regla: Para cada 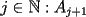 es la unión de es la unión de 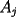 con el conjunto de todos los puntos de corte de con el conjunto de todos los puntos de corte de 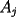 . Pruebe que, si la unión de todos los conjuntos de la sucesión es un conjunto finito, entonces todos los términos de la sucesión son iguales a . Pruebe que, si la unión de todos los conjuntos de la sucesión es un conjunto finito, entonces todos los términos de la sucesión son iguales a 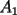 . .Resumen de soluciones: -------------------- |
|
|
|
 Apr 5 2007, 03:57 PM Apr 5 2007, 03:57 PM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Solución al problema 4
Podemos escribir 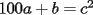 y y 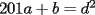 , donde , donde 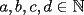 , con , con 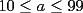 , , 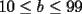 y y 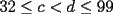 . Ahora, el truco "evidente" (para quien tiene experiencia en estos tipos de problemas) es restar ambas igualdades, y luego factorizar el lado derecho: . Ahora, el truco "evidente" (para quien tiene experiencia en estos tipos de problemas) es restar ambas igualdades, y luego factorizar el lado derecho: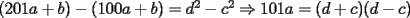 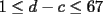 , entonces 101 no divide a , entonces 101 no divide a 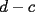 . Pero 101 es primo, entonces . Pero 101 es primo, entonces 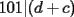 . Ahora acotamos esta suma: . Ahora acotamos esta suma: 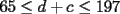 , entonces obtenemos las siguientes conclusiones: , entonces obtenemos las siguientes conclusiones: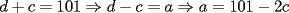 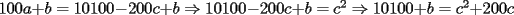 . Nada nos impide completar el cuadrado, en el lado derecho de la igualdad, para lo cual debemos sumar 10000 . Nada nos impide completar el cuadrado, en el lado derecho de la igualdad, para lo cual debemos sumar 10000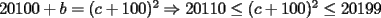 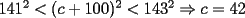 , y por lo tanto , y por lo tanto 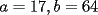 (solución única) (solución única)
-------------------- |
|
|
|
 Apr 9 2007, 03:36 PM Apr 9 2007, 03:36 PM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Solución al problema 3
Caso 1:  es impar y potencia de primo (ie: existen es impar y potencia de primo (ie: existen 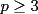 , primo, y , primo, y 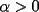 , entero, tales que , entero, tales que 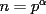 ) )Considere 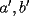 cualesquiera, tales que cualesquiera, tales que 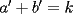 . Como . Como  , entonces al menos una de las representaciones: , entonces al menos una de las representaciones: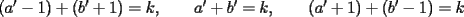 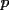 . Esa será nuestra representación . Esa será nuestra representación 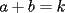 Caso 2:  impar, cualquiera impar, cualquieraEscribimos 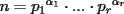 , donde , donde 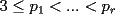 son números primos, y son números primos, y 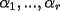 son números enteros positivos. son números enteros positivos.Para cada 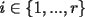 , escriba , escriba 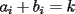 , de modo que , de modo que 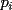 no divida a no divida a 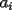 ni a ni a 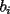 (esto se puede hacer, por el caso 1). Por el teorema chino de los restos, existen (esto se puede hacer, por el caso 1). Por el teorema chino de los restos, existen 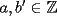 tales que: tales que: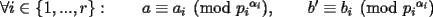 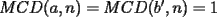 . Además, ocurre lo siguiente: . Además, ocurre lo siguiente: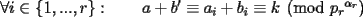 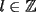 tal que tal que 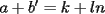 . Definiendo . Definiendo 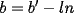 , tenemos que , tenemos que 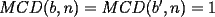 y también que y también que 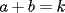 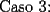 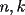 son pares son paresEscriba 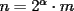 , con , con 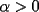 , entero, y , entero, y 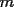 impar. Por el caso anterior, existen impar. Por el caso anterior, existen 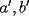 enteros tales que enteros tales que 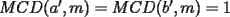 y y 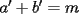 . Si . Si 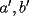 son impares, entonces considere son impares, entonces considere 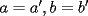 . De lo contrario, considere . De lo contrario, considere 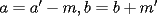 Comentario 1: No siempre podemos tener 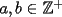 , independiente del valor de , independiente del valor de 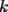 . Basta que . Basta que  tenga una gran cantidad de divisores primos pequeños (por ejemplo, si tenga una gran cantidad de divisores primos pequeños (por ejemplo, si 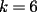 y y 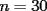 , entonces , entonces 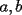 tienen signos opuestos) tienen signos opuestos)Comentario 2: Si  es par y es par y 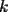 es impar, entonces no pueden existir es impar, entonces no pueden existir 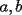 . De hecho: . De hecho: 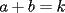 implica que 2 divide a implica que 2 divide a  , o bien 2 divide a , o bien 2 divide a 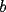
-------------------- |
|
|
|
 Mar 14 2010, 06:28 PM Mar 14 2010, 06:28 PM
Publicado:
#4
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Problema 2: Considere (fijos en el plano) una circunferencia, y un punto 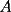 exterior a ella. Sea exterior a ella. Sea 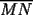 un diámetro variable. Encuentre el LG del circuncentro del un diámetro variable. Encuentre el LG del circuncentro del 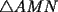 al variar al variar 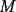 . .Sean 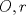 el centro y el radio de la circunferencia fija, respectivamente. Construyamos ejes perpendiculares, que posean a el centro y el radio de la circunferencia fija, respectivamente. Construyamos ejes perpendiculares, que posean a 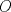 como origen, y que como origen, y que 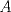 esté ubicado sobre el eje y. Pongamos esté ubicado sobre el eje y. Pongamos 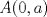 , , 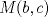 , , 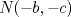 , con , con 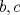 reales tales que reales tales que 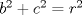 . No es difícil ver que las mediatrices de . No es difícil ver que las mediatrices de 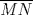 , , 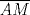 tienen por ecuaciones tienen por ecuaciones 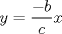 e e  , respectivamente. Resolviendo el sistema, obtenemos que el circumcentro del , respectivamente. Resolviendo el sistema, obtenemos que el circumcentro del  tiene por coordenadas tiene por coordenadas 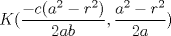 . El valor de la ordenada de . El valor de la ordenada de  (es decir, (es decir, 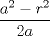 ) es constante independiente de las posiciones de ) es constante independiente de las posiciones de  sobre la circunferencia. Como este valor indica la distancia de sobre la circunferencia. Como este valor indica la distancia de  al eje al eje  , obtenemos que la distancia de , obtenemos que la distancia de  al eje al eje  es constante para todas las posiciones de es constante para todas las posiciones de 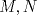 , o sea, , o sea, 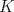 se mueve sobre una recta paralela al eje se mueve sobre una recta paralela al eje  . . Ahora probaremos que todo punto de la recta 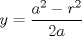 es el lugar geométrico buscado. En efecto, la abscisa de es el lugar geométrico buscado. En efecto, la abscisa de  , , 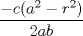 equivale a equivale a 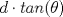 donde donde  es el ángulo en que la recta es el ángulo en que la recta 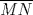 corta al eje corta al eje  y y 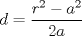 es una constante. Considerando que la función tangente es surjectiva en los reales, obtenemos que todo punto de la recta es una constante. Considerando que la función tangente es surjectiva en los reales, obtenemos que todo punto de la recta 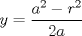 es el lugar geometrico buscado. es el lugar geometrico buscado.Si llamamos  a esa recta, es claro que a esa recta, es claro que 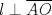 . Finalmente, si llamamos . Finalmente, si llamamos 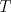 al punto al interior del segmento al punto al interior del segmento 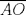 tal que tal que 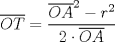 , y con todo lo expuesto, obtenemos que el lugar geometrico de los circumcentros es una recta perpendicular a , y con todo lo expuesto, obtenemos que el lugar geometrico de los circumcentros es una recta perpendicular a 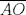 que pasa por el punto que pasa por el punto 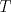 . . Todo el manejo "algebraico" se deja a manos del atento lector -------------------- Ricardo Vargas Obando
Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile.  Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico:
|
|
|
|
 Mar 15 2010, 08:43 PM Mar 15 2010, 08:43 PM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Sólo pude comprobar hasta que el sistema de ecuaciones fue bien resuelto, por lo tanto el lugargeométrico buscado debería ser una recta (es decir, pude comprobar una de las inclusiones). No hay problemas con a ni con a-c en el denominador, pero sí debe ser explicado lo que sucede con b o c iguales a 0.
Tampoco está de más recordar que esperamos una solución con geometría euclidiana (y también con otras técnicas no utilizadas hasta aquí en el tema) -------------------- |
|
|
|
 Nov 21 2011, 11:09 AM Nov 21 2011, 11:09 AM
Publicado:
#6
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 217 Registrado: 5-April 11 Desde: no se :c Miembro Nº: 86.300 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Problema 1
Notemos que si consideramos un rectángulo de 1x5 (5 casillas) siempre estará contenido en otro rectángulo de 1x6 (6 casillas). Como cada 6 casillas al menos debe haber 2 adyacentes coloreadas, entonces como mínimo, un rectángulo de 1x5 debe tener 3 casillas coloreadas. Luego, si retiramos una de las casillas de la esquína del tablero de 1001x1001 que no esté coloreada, podemos ubicar los rectángulos de 1x5 si problemas, ya que: 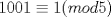 entonces entonces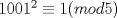 Entonces si por cada rectángulo de 1x5 hay un mínimo de 3 casillas coloreadas, entonces en todo el tablero, el mínimo de casillas coloreadas estará dado por:  · · 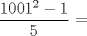  · · 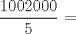 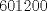 Respondiendo lo pedido. Salu2 -------------------- Cuando eliminamos lo imposible lo que queda, por improbable que parezca...siempre será la verdad...
Nada tiene sentido, pero todo tiene significado. |
|
|
|
 Nov 21 2011, 05:04 PM Nov 21 2011, 05:04 PM
Publicado:
#7
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 193 Registrado: 22-March 07 Desde: San Miguel, Santiago Miembro Nº: 4.651 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Problema 1 Notemos que si consideramos un rectángulo de 1x5 (5 casillas) siempre estará contenido en otro rectángulo de 1x6 (6 casillas). Como cada 6 casillas al menos debe haber 2 adyacentes coloreadas, entonces como mínimo, un rectángulo de 1x5 debe tener 3 casillas coloreadas. Luego, si retiramos una de las casillas de la esquína del tablero de 1001x1001 que no esté coloreada, podemos ubicar los rectángulos de 1x5 si problemas, ya que: 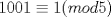 entonces entonces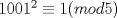 Entonces si por cada rectángulo de 1x5 hay un mínimo de 3 casillas coloreadas, entonces en todo el tablero, el mínimo de casillas coloreadas estará dado por:  · · 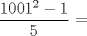  · · 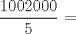 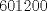 Respondiendo lo pedido. Salu2 creo que debes ser un poco mas riguroso en explicar por que son como minimo 3 coloreadas en un rectangulo de 5x1, explicar si es alcanzable el minimo (alguna justificacion o la forma de colorear) saludos! -------------------- |
|
|
|
 Nov 22 2011, 12:41 PM Nov 22 2011, 12:41 PM
Publicado:
#8
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 217 Registrado: 5-April 11 Desde: no se :c Miembro Nº: 86.300 Nacionalidad:  Colegio/Liceo:  Sexo:  |
creo que debes ser un poco mas riguroso en explicar por que son como minimo 3 coloreadas en un rectangulo de 5x1, explicar si es alcanzable el minimo (alguna justificacion o la forma de colorear) saludos! Consideremos un rectángulo de 1x6, deletreadas desde A hasta F, donde están contenidos 2 rectángulos de 1x5 (A hasta E, y B hasta F). Sabemos que por cada rectángulo de 1x6 necesariamente deben existir dos casillas adyacentes coloreadas, en nuestro rectángulo de 1x6, tenemos 5 posibilidades de colorearlas: AB, BC, CD, DE, EF. La primera condición nos dice que de por cada casilla adyacente, debe existir 2 al menos una coloreada, por lo tanto en los cinco casos, considerando las casillas adyacentes coloreadas (AB, BC, CD, DE, EF ), colorearemos la menor cantidad de casillas posibles cumpliendo el enunciado: Caso AB: la casilla D es adyacente a C y E, y F es adyacente a E, por lo tanto coloreamos D y F. Caso BC: tenemos que B y C son adyacentes a A y D respectivamente, pero ya están coloreadas, y E es adyacente a D y F, por lo tanto, coloreamos E. Caso CD: con C y D coloreadas, podemos colorear A, que es adyacente a B, y F que es adyacente a F. Caso DE: tenemos que B es adyacente a A y C, y tenemos que E (coloreada) es adyacente a F. Coloreamos B. Caso EF: coloreando A y C, cubrimos a AB y CD. Notemos que en todos los casos, siempre los rectángulos de 1x5 (desde A hasta E o bien desde B hasta F) quedan 3 casillas coloreadas. Mensaje modificado por MatíasMoreno el Nov 22 2011, 12:44 PM
Archivo(s) Adjunto(s)
-------------------- Cuando eliminamos lo imposible lo que queda, por improbable que parezca...siempre será la verdad...
Nada tiene sentido, pero todo tiene significado. |
|
|
|
 Jun 8 2013, 06:36 PM Jun 8 2013, 06:36 PM
Publicado:
#9
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.116 Registrado: 12-March 11 Miembro Nº: 84.732 Nacionalidad:  Sexo:  |
P5
Trazamos el circuncirculo del 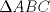 con centro con centro 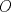 . Por . Por 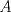 trazamos una tangente a la circunferencia de manera que corte al lado opuesto, trazamos una tangente a la circunferencia de manera que corte al lado opuesto, 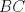 , en , en 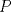 . En la contruccion que muestra el dibujo vemos claramente que como . En la contruccion que muestra el dibujo vemos claramente que como 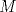 es punto medio del es punto medio del 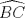 entonces entonces 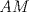 es bisectriz del es bisectriz del 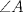 . Luego . Luego 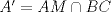 . El . El 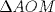 es isosceles y si llamamos es isosceles y si llamamos  a sus angulos basales tenemos que: a sus angulos basales tenemos que: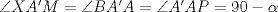 . .De esta manera vemos que el 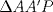 es isosceles en es isosceles en 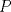 , con lo cual la mediatriz de , con lo cual la mediatriz de  , que nos pide el enunciado, intercepta al lado , que nos pide el enunciado, intercepta al lado 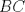 en en 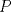 , con lo cual , con lo cual 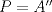 . Podriamos hacer lo mismo en los vertices . Podriamos hacer lo mismo en los vertices 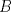 y y 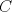 y encontrariamos, respectivamente, que sus tangentes interceptan los lados opuestos en los puntos y encontrariamos, respectivamente, que sus tangentes interceptan los lados opuestos en los puntos 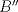 y y 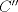 que nos indica el enunciado. Luego podemos aplicar uno de los casos limites del Teorema de Pascal que dice: que nos indica el enunciado. Luego podemos aplicar uno de los casos limites del Teorema de Pascal que dice:"En todo triángulo inscrito en una cónica (aqui su circuncirculo), los puntos de intersección de los lados con las tangentes trazadas en los vértices opuestos son tres puntos en línea recta". --------------------------- "Teorema de Pascal" (Casos limites): http://garciacapitan.99on.com/bella/htm/juntos.htm
Archivo(s) Adjunto(s)
-------------------- |
|
|
|
 Sep 8 2013, 01:32 PM Sep 8 2013, 01:32 PM
Publicado:
#10
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 217 Registrado: 5-April 11 Desde: no se :c Miembro Nº: 86.300 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Ahora no les debo imágen, saludos
Problema 5: -------------------- Cuando eliminamos lo imposible lo que queda, por improbable que parezca...siempre será la verdad...
Nada tiene sentido, pero todo tiene significado. |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 16th June 2025 - 08:30 AM |





 es coprimo con
es coprimo con  y con
y con 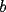
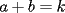








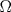 como el circuncírculo del
como el circuncírculo del 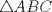 , vamos a demostrar primero que las rectas
, vamos a demostrar primero que las rectas  ,
, 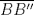 y
y 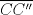 son tangentes a
son tangentes a 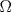 , sean
, sean 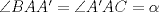 ,
, 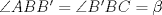 y
y 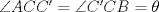 y comencemos a mover ángulos, es fácil ver que los triángulos
y comencemos a mover ángulos, es fácil ver que los triángulos 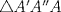 ,
, 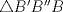 ,
, 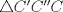 son isósceles, ya que A'', B'', C'' están en las mediatrices de
son isósceles, ya que A'', B'', C'' están en las mediatrices de 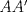 ,
, 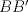 ,
, 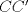 respectivamente, de esto tenemos que
respectivamente, de esto tenemos que 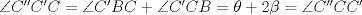 , pero como
, pero como 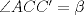 , se tiene que
, se tiene que 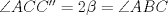 , luego
, luego 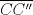 es tangente a
es tangente a 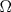 , y de forma análoga obtenemos que
, y de forma análoga obtenemos que 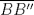 ,
, 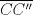 son tangentes a
son tangentes a 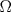 , luego sea
, luego sea 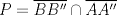 ,
, 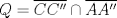 y
y 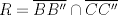 , como
, como 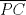 ,
, 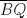 y
y 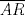 son concurrentes, entonces los triángulos
son concurrentes, entonces los triángulos 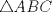 y
y 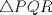 son perspectivos respecto al punto de concurrencia, luego notemos que
son perspectivos respecto al punto de concurrencia, luego notemos que 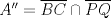 ,
, 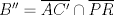 y
y 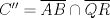 , que son coolineales en consecuencia directa del Teorema de Desargues, con esto finalizamos
, que son coolineales en consecuencia directa del Teorema de Desargues, con esto finalizamos 