|
|
|
|
|
|
|
  |
 Oct 24 2010, 08:15 PM Oct 24 2010, 08:15 PM
Publicado:
#31
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Esta fue la ultima vez que compito en la Olimpiada Nacional de Matemática y estoy contento por la medalla de oro que obtuve
Problema 1: Problema 2: Problema 3: Problema 4: Problema 5: Felicitaciones a todos!!!! En especial a Hamon por su verganza exitosa, a Pedantic por su medalla de Oro. Adios -------------------- Ricardo Vargas Obando
Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile.  Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico:
|
|
|
|
 Oct 25 2010, 01:54 PM Oct 25 2010, 01:54 PM
Publicado:
#32
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 1 Registrado: 20-October 10 Miembro Nº: 78.991 Nacionalidad:  Sexo:  |
Problema 6
(perdonen el paint. última vez)  dibujox0.png ( 623.48k )
Número de descargas: 1
dibujox0.png ( 623.48k )
Número de descargas: 1 dibujox.png ( 623.48k )
Número de descargas: 1
dibujox.png ( 623.48k )
Número de descargas: 1![TEX: Entonces, el largo del segmento $x$ (en la figura 1) es:<br />\[x = 2010 r - 2 r({\sqrt{3}-1})\]<br />Y la cantidad de circunferencias cuyos centros pertenecen al segmento x, y son tangentes a la base, son<br />\[ [{{2010 r - 2 r({\sqrt{3}-1})}\over 2r}] = 1004\]<br />donde [] corresponde a la función parte entera.](./tex/e0e98111918501b2f4706e7522ceae10.png)  DIBUJO4.PNG ( 483.9k )
Número de descargas: 1
DIBUJO4.PNG ( 483.9k )
Número de descargas: 1![TEX: <br />Con esto demostramos que cuando disponemos un círculo tangente a dos del nivel inferior, la diferencia de altura entre los centros es $r \cdot \sqrt{3}$. Lo que implica que el largo del segmento $x$ que pasa por los centros de un nivel $m+1$, es $2r$ menos que el nivel $m$. Entonces, en el nivel $m+1$ cabe una circunferencia menos que en el nivel $m$.<br /><br />En total, caben $\sum_{i=1}^{1004}{i}$ circunferencias dentro del triángulo. Y el área de ellas juntas es<br />\[ {{1004 \over 2} \cdot 1005 \cdot \pi \cdot a^{2}} \over {2010^2} \]<br /><br />Como $\pi > 3,1$ y $\sqrt{3} < 1,8$, tenemos que <br />\[ {{{1004 \over 2} \cdot 1005 \cdot \pi \cdot a^{2}} \over {2010^2}} > {{{1004 \over 2} \cdot 1005 \cdot 3,1 \cdot a^{2}} \over {2010^2}} > {{{17 \cdot 1,8 \cdot a^2} \over 2010}} > {{{17 \sqrt{3}} \over 2010} a^2} \] <br />lo que demuestra la proposición.](./tex/b9a876aeb99ea1e49132c3b0d89ff200.png)
Mensaje modificado por igorabarzua el Oct 25 2010, 01:57 PM |
|
|
|
 Oct 25 2010, 02:06 PM Oct 25 2010, 02:06 PM
Publicado:
#33
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad:  Colegio/Liceo:  Sexo:  |
encontre como ultra fome ese problema, porque como que te daba todo, y solo habia que reescribir las cosas y usar dos formulas... por eso no quise poner una solucion aca y ahora veo que era tan fome como yo pensaba xddddddd
-------------------- |
|
|
|
 Oct 25 2010, 09:18 PM Oct 25 2010, 09:18 PM
Publicado:
#34
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 143 Registrado: 6-February 08 Desde: desde aquí Miembro Nº: 15.300 Nacionalidad:  Colegio/Liceo:  Sexo:  |
encontre como ultra fome ese problema, porque como que te daba todo, y solo habia que reescribir las cosas y usar dos formulas... por eso no quise poner una solucion aca y ahora veo que era tan fome como yo pensaba xddddddd Pensé lo mismo... en verdad creo que había visto una muy parecido antes de irme a santiago y fue como "caido del cielo" el problema xD -------------------- |Ente Inmiscible|  |
|
|
|
 Oct 25 2010, 09:30 PM Oct 25 2010, 09:30 PM
Publicado:
#35
|
|
 Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 1.559 Registrado: 18-November 07 Miembro Nº: 12.754 Nacionalidad:  Sexo:  |
Esta fue la ultima vez que compito en la Olimpiada Nacional de Matemática y estoy contento por la medalla de oro que obtuve Felicitaciones a todos!!!! En especial a Hamon por su verganza exitosa, a Pedantic por su medalla de Oro. No me queda más que felicitarte pro el oro, te dije que lo sacarías!! Sería bonito volver al CPEIP, como parte del comité de la ONM, en hartos años más Gracias por las felicitaciones. A ver si hacemos otro tema, como el del año pasado,exclusivo para conversar sobre la ONM 2010 final. Saludos! -------------------- Empezando con Desigualdades? Encuentra aquí problemas resueltos
|
|
|
|
 Oct 25 2010, 09:48 PM Oct 25 2010, 09:48 PM
Publicado:
#36
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.169 Registrado: 11-June 08 Desde: rancagua Miembro Nº: 26.922 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
No me queda más que felicitarte pro el oro, te dije que lo sacarías!! Sería bonito volver al CPEIP, como parte del comité de la ONM, en hartos años más Gracias por las felicitaciones. A ver si hacemos otro tema, como el del año pasado,exclusivo para conversar sobre la ONM 2010 final. Saludos! -------------------- Richard Fabian Jerez
Ex alumno del Liceo Oscar Castro 4ºL matemático ¿Necesitas ayuda para la psu y no tienes dinero?: Agrega a logratus850@hotmail.com y comienza a preguntar! Somos un grupo de universitarios dispuestos a ayudarte de manera gratuita para que logres tus sueños, todos tuvimos como promedio más de 800 puntos en la PSU. Team PSU 2010!! Únete!  [color="#000080"][/color] [color="#000080"][/color] |
|
|
|
 Oct 26 2010, 05:26 PM Oct 26 2010, 05:26 PM
Publicado:
#37
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 688 Registrado: 8-November 09 Desde: Villarrica Miembro Nº: 61.657 Nacionalidad:  Colegio/Liceo:  Universidad: .png) Sexo:  |
Felicitaciones a todos!!!! En especial a Hamon por su verganza exitosa, a Pedantic por su medalla de Oro. Adios Gracias Ricardo felicidades a ti tambien. Me sumo a las felicitaciones a Hamon, y a todos los demas usuarios que sacaron algo. Que lata que no haya ninguno mas en el nvl menor D: Mensaje modificado por Pedantic Anarchy el Oct 26 2010, 05:36 PM -------------------- yo no soy especial
a pesar que ella lo dijo tengo unos krk y un celular hechizo aún vácilo SFDK en el segundo piso y la frase final da igual la improviso |
|
|
|
 Oct 26 2010, 05:43 PM Oct 26 2010, 05:43 PM
Publicado:
#38
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 143 Registrado: 6-February 08 Desde: desde aquí Miembro Nº: 15.300 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Esta fue la ultima vez que compito en la Olimpiada Nacional de Matemática y estoy contento por la medalla de oro que obtuve Felicitaciones a todos!!!! En especial a Hamon por su verganza exitosa, a Pedantic por su medalla de Oro. Adios Ese Adiós me sonó melancólico.... -------------------- |Ente Inmiscible|  |
|
|
|
 Oct 26 2010, 10:44 PM Oct 26 2010, 10:44 PM
Publicado:
#39
|
|
 Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 29 Registrado: 29-June 08 Desde: Santiago Centro Miembro Nº: 28.578 Nacionalidad:  Colegio/Liceo:  Sexo:  |
MAESTROS!
Es un HONOR HABER COMPETIDO CON USTEDES EN TANTA ,VALGA LA REDUNDANCIA, COMPETENCIA .. De Verdad. Felicitaciones y aunque no me destaco tanto en el foro.. soy un apasionado por esta bella ciencia.... SALUDOS Y REITERO.... FELICITACIONES MUCHACHOS --------------------  |
|
|
|
 Feb 19 2011, 05:39 PM Feb 19 2011, 05:39 PM
Publicado:
#40
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 1 Registrado: 19-February 11 Miembro Nº: 83.944 |
Mi respuesta al P4, no sé que tengo mal, me ayudan?:
m+n√2=(1+√2)^{2010} (1+√2)^{2010} = 1+√2+2+√2^{3}+4+...√2^{2009}+2^{1005} entonces 1+2+4+8...2^{1005}+√2(1+2+4...2^{1004} entonces hice la demostracion: 2^{n}+2^{n+2} divisible por 5. 2^{n}+2^{n+2} 2^{n}+4(2^{n}) 5(2^{n}) Q.E.D. Entonces, pasa lo siguiente: 1+2+4+8+16... 1+4 divisible por 5 2+8 idem 4+16 etc. En rigor, cada 4 potencias de 2 sumadas, son divisibles por 5 entonces en el problema original m+n√2=(1+√2)^{2010} N = 1+2+4...2^{1004} es decir 2^{0}+2^{1}+2^{2}...2^{1004} 1005 potencias de 2 1005/4= X resto = 1 gracias de antemano! Mensaje modificado por Gerbo el Feb 19 2011, 05:39 PM |
|
|
|
  |
2 usuario(s) está(n) leyendo esta discusión (2 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 30th April 2025 - 01:09 PM |





 . Una desigualdad bastante "sencilla".
. Una desigualdad bastante "sencilla". ,
,  ,
,  . Sean además
. Sean además 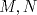 los puntos medios de
los puntos medios de 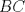 y
y 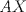 , respectivamente. Denotemos por
, respectivamente. Denotemos por 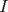 al incentro del
al incentro del 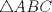 . Si
. Si 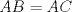 , tendríamos que
, tendríamos que 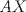 sería la mediatriz de
sería la mediatriz de 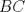 y la bisectriz del
y la bisectriz del 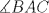 , y que
, y que  , de donde es directo que
, de donde es directo que 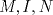 son colineales. En otro caso, si
son colineales. En otro caso, si 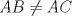 , asumamos sin pérdida de generalidad que
, asumamos sin pérdida de generalidad que 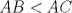 .
. 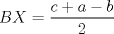 ,
, 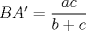 y
y 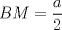 . Como
. Como 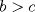 , se sigue que
, se sigue que 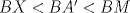 . Esto quiere decir que los puntos
. Esto quiere decir que los puntos 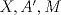 aparecen en ese orden sobre
aparecen en ese orden sobre 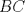 . Entonces, por el teorema de Menelao aplicado al
. Entonces, por el teorema de Menelao aplicado al 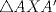 y puntos
y puntos 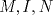 , se sigue que
, se sigue que 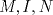 serán colineales si y solo si
serán colineales si y solo si 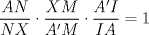
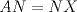 ,
, 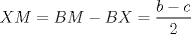 ,
, 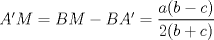 y que por el Teorema de la Bisectriz aplicada al
y que por el Teorema de la Bisectriz aplicada al 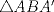 se tiene que
se tiene que 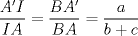 .
. 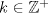 , sea
, sea 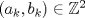 tal que
tal que 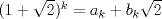 . Demostraremos que
. Demostraremos que 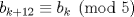 . En efecto,
. En efecto, 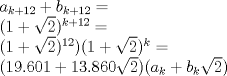
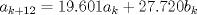 y
y 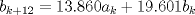 . Es directo de esto último que
. Es directo de esto último que 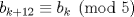 . Como
. Como 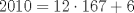 se sigue que el resto de
se sigue que el resto de 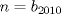 módulo
módulo 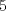 es el mismo que deja
es el mismo que deja 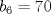 , el cual es cero. Por lo tanto
, el cual es cero. Por lo tanto  es múltiplo de
es múltiplo de 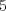
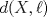 la distancia de un punto
la distancia de un punto 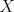 a una recta
a una recta 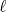 . Suponga que
. Suponga que 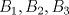 aparecen en ese orden sobre
aparecen en ese orden sobre 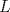 . Sean
. Sean 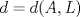 ,
, 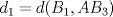 y
y 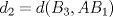 .
.  denota el área de un triángulo
denota el área de un triángulo 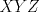
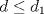 y
y 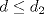 . Entonces
. Entonces 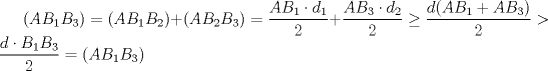
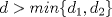 y estamos listos.
y estamos listos.







