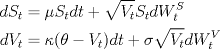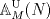* Ejercicio muy bonito - Foro fmat.cl

* Ejercicio muy bonito, Un criterio de normalidad en grupos finitos

rfauffar Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 25 2009, 11:52 PM Publicado: #1
Maestro Matemático Grupo: Usuario FMAT Mensajes: 94 Registrado: 2-March 07 Desde: Santiago Miembro Nº: 4.247 Nacionalidad: Sexo:	$TEX: Demuestre que si $H$ es subgrupo de un grupo $G$ de \'{\i}ndice $p$ primo, donde $p$ es el menor primo que divide el orden de $G$, entonces $H$ es normal.$ -------------------- Romanos 5:6-8 6 Cuando nosotros los pecadores no podíamos salvarnos, Cristo murió por nosotros ..... 7 En realidad, no es fácil que alguien esté dispuesto a morir en lugar de otra persona, aunque sea buena y honrada. Tal vez podríamos encontrar a alguien que diera su vida por alguna persona realmente buena.8 Pero aunque nosotros todavía éramos pecadores, Dios nos demostró su gran amor al enviar a Jesucristo a morir por nosotros. Efesios 2:8-9 8 Ustedes han sido salvados porque aceptaron el amor de Dios. Ninguno de ustedes se ganó la salvación, sino que Dios se la regaló.9 La salvación de ustedes no es el resultado de sus propios esfuerzos. Por eso nadie puede sentirse orgulloso. Robbie Auffarth Licenciatura en Matemáticas Pontificia Universidad Católica de Chile

coquitao Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 26 2009, 04:51 PM Publicado: #2
Dios Matemático Supremo Grupo: Super Moderador Mensajes: 2.065 Registrado: 25-May 08 Desde: Pelotillehue Miembro Nº: 24.463	Notar que la propuesta de rfauffar nos proporciona una nueva solución (en el caso finito) a la propuesta de acá. Saludos. Mensaje modificado por coquitao el Apr 26 2009, 04:59 PM -------------------- "Please forget everything you have learned in school; for you haven't learned it... Please keep in mind at all times the corresponding portions of your school curriculum; for you haven't actually forgotten them." -- E. Landau

coquitao Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 18 2009, 01:02 AM Publicado: #3
Dios Matemático Supremo Grupo: Super Moderador Mensajes: 2.065 Registrado: 25-May 08 Desde: Pelotillehue Miembro Nº: 24.463	Vamos a presentar la solución más elemental posible de este resultado. Nada de acciones ni demáses. Sólo requeriremos del siguiente resultado preliminar: Lema. Si a un elemento de 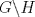$TEX: $G \backslash H$$ , entonces las clases laterales $TEX: $H, aH, \ldots, a^{p-1}H$$ son disjuntas dos a dos. Prueba. ¿Quién se anima a escribirla? Una vez demostrado este resultado preliminar procedemos a probar la normalidad del subgrupo H. Sea b un elemento de 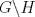$TEX: $G \backslash H$$ . 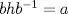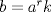Si $TEX: $bhb^{-1}=a$$ no estuviera en H, el lema preliminar nos aseguraría la existencia de un natural r y un elemento k de H tal que $TEX: $b=a^{r}k$$ . 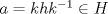Se tendría entonces que $TEX: $a=khk^{-1} \in H$$ , lo cual entraría en contradicción con la suposición hecha sobre $TEX: $a$$ y de ahí la normalidad del subgrupo H. QED. -- Importante: Todas las dudas sobre la notación empleada se pueden disipar visitando este post. -------------------- "Please forget everything you have learned in school; for you haven't learned it... Please keep in mind at all times the corresponding portions of your school curriculum; for you haven't actually forgotten them." -- E. Landau

Abu-Khalil Ver Perfil del Miembro Ver los mensajes de este miembro	Sep 30 2009, 08:51 PM Publicado: #4
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Notar que acá también se guía su desarrollo. -------------------- ~milopez $TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]$ $TEX: <br />\begin{equation}\begin{aligned}<br />dS_t&=\mu S_t dt+\sqrt{V_t}S_t dW^S_t\\<br />dV_t&=\kappa(\theta-V_t)dt+\sigma\sqrt{V_t} dW^V_t\\<br />\end{aligned}\end{equation}<br />$ $TEX: <br />$$\mathbb A^{\text U}_M(N)$$<br />$

coquitao Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 1 2009, 02:01 PM Publicado: #5
Dios Matemático Supremo Grupo: Super Moderador Mensajes: 2.065 Registrado: 25-May 08 Desde: Pelotillehue Miembro Nº: 24.463	CITA(Abu-Khalil @ Sep 30 2009, 08:51 PM) Notar que acá también se guía su desarrollo. Tienes toda la razón, estimado Abu. Ya me había percatado de la existencia de dicho tema, pero la prueba esbozada ahí no me gustó tanto como la que aparece aquí arribita. Si K es el kernel del homomorfismo F entonces K es un subgrupo normal de G que está contenido en H. Además, G/K es isomorfo a un subgrupo de 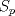$TEX: $S_{p}$$ y de ahí que [G:K] sea un divisor de p!. Dado que cada divisor de [G:K] es divisor de \|G\| se sigue que [G:K] = p ó [G:K] = 1. Luego, el post de aquí nos permite asegurar que $TEX: $[G:K] = [G:H][H:K] = p[H:K] \geq p$$ y por tanto [H:K] = 1. De esto último se sigue que H = K y el resultado se tiene entonces como consecuencia de la normalidad de K. QED. ¿Cuál de las dos pruebas presentadas hasta el momento prefieren ustedes, estimados usuarios? -------------------- "Please forget everything you have learned in school; for you haven't learned it... Please keep in mind at all times the corresponding portions of your school curriculum; for you haven't actually forgotten them." -- E. Landau

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Fecha y Hora actual: 29th October 2025 - 07:42 PM